We thus find that the voltage of the sector Vp must be equal to the product of the number 4.45 by the frequency f, by the maximum value Φ of the flux and by the number of turns of the primary Np.
To determine this number of turns, it suffices to divide the voltage of the sector by the product of 4.45 by the frequency and by the maximum value of the flux ; the mains voltage and the frequency are always known, it remains to seek the maximum value of the flow, which we will see later.
All this shows us that the number of turns of the primary is even greater than the effective value of the voltage that we want to apply to the transformer is greater. To use a transformer with different network voltages, it is sufficient to vary the number of primary turns to which each of these voltages is applied.
The Figure 4 shows, for example, how one can use the transformers of Figure 3 above with a mains voltage of 110 V.
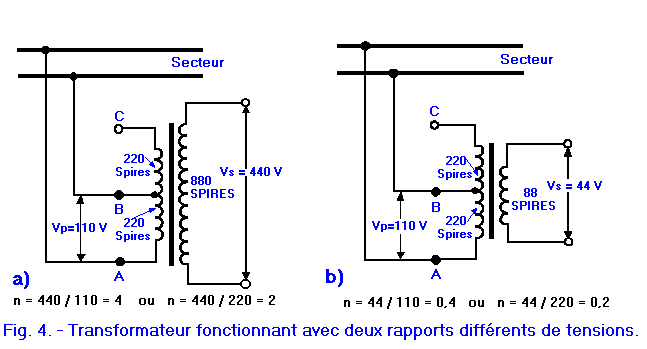
Since the voltage of 220 V applies to each of the 440 turns of the primary, the voltage of 110 V, a value equal to half of the previous one, must apply to a number of turns equal to half the previous, that is to say only 220 turns. For this purpose, an intermediate tap (indicated by B in Figure 4) is used arranged between the end A of the winding and this tap to include the 220 turns required, while the 220 turns of the coil winding which remain between the end (C) and the socket B are not used.
In this way, the transformation ratio of these transformers is doubled : indeed, if we compare Figure 3 and Figure 4, we see that for the step-up transformer, the transformation ratio goes from 2 to 4, while for the step-down transformer, the same ratio goes from 0.2 to 0.4.
Many transformers have a primary having a plurality of intermediate taps, each being adapted to a particular voltage value; these primaries are called universal because they allow to use the transformer with all the possible values that can take the tension of the sector.
It is also possible to use the intermediate sockets for the secondary, when lower voltages are required than the one obtained at the ends of the winding : for example, with a socket located at the half of the secondary of the transformer of the Figure 4-a, one could obtain two voltages of 220 V, between this socket and each end of the winding.
 1. 3. - OPERATION IN CHARGE OF THE TRANSFORMER
1. 3. - OPERATION IN CHARGE OF THE TRANSFORMER
We will now see how the operation of the transformer changes when its secondary is connected to the circuit which must be powered by the voltage Vs provided by the winding.
Under these conditions, it is said that the transformer operates in load because the circuit connected to its secondary is also called transformer load.
Assuming that this circuit comprises only a "resistor", as in Figure 5, the secondary voltage Vs will circulate there a secondary current (indicated by Is) whose intensity is equal to the secondary voltage divided by the value of resistance, according to OHM law. Since this current flows through the load constituted by the resistor, it is also called the load current.
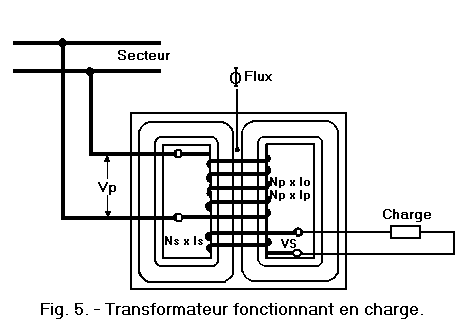
By circulating in the turns of the secondary, the charging current in turn produces an induction flux able to oppose, according to Lenz's law, to the cause that generated it, that is to say to the variation of the flow Φ produced by the magnetization current Io.
One could thus think that the flow produced by the secondary current by opposing the variation of the flow Φ produced by the magnetization current, makes the operation of the transformer impossible ; but on the contrary, as soon as the circulation of the secondary current (Is) begins and so that the flow occurs, the primary takes to the network a new current, which we indicate by Ip, and thus produces in its turn a third flow which, at every moment is equal and opposite to that produced by the secondary current, and so neutralizes the effect.
This is the phenomenon of mutual induction according to which, as we have already seen, the windings act one on the other : indeed, just as the primary determines the circulation of the current Is in the secondary, so the secondary, in turn, determines the flow of current Ip in the primary.
As the two flows produced by these currents are equal and opposite, they cancel each other out and when the transformer operates under load, it has practically in its core that the flux &€934; produced by the magnetization current Io, as in the case of the operation empty.
Note that when the transformer operates at full load, the current Io is much lower than the current Ip ; that is why we will limit ourselves henceforth to the examination of this current.
Since these two flows are equal, the f.m.m. who produce them must also be equal : the f.m.m. primary, indicated by the product Np x Ip in Figure 5, must be equal to the f.m.m. secondary, indicated by the product Ns x Is in this same figure 5.
This equality between the f.m.m. allows to see what relation exists between the number of turns of primary and secondary and between the corresponding currents Ip and Is.
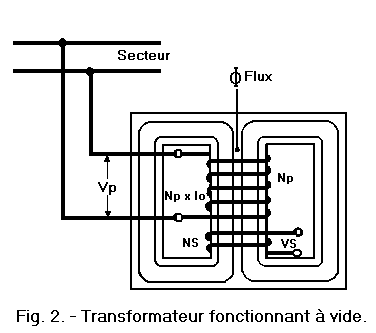
Let us see for this figure 6, where are shown the transformers of Figure 3 ; the secondary ones are now connected to "resistances" of a value allowing to circulate the same load current of 2 amps.
As the secondary of the transformer of Figure 6-a comprises 880 turns, the f.m.m. due to the current of 2 amps circulating in this winding is 880 x 2 = 1760 A.t.
On the other hand, since the primary of this transformer has a number of turns equal to half that of the secondary (440 instead of 880), to produce the same f.m.m. this winding must be traversed by a current twice as large as that of the secondary, that is to say by a current of 4 amps : in fact, in this case, we still obtain 440 x 4 = 1760 A.t.
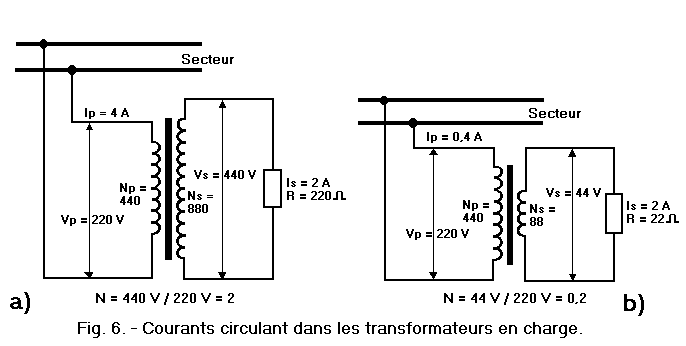
We see that the transformer raises the value of the voltage, doubling it from 220 to 440 V, but that it reduces in the same ratio the intensity of the current, lowering it indeed by 4 to 2 A.
For the transformer of Figure 6-b, the f.m.m. of the secondary is equal to 88 x 2 = 176 A.t because its winding has only 88 turns traveled by the current of 2 amps.
To produce the same fmm, the primary which has a number of turns five times larger than the secondary (440 instead of 88), must be traversed by a current five times smaller than that of the secondary, thus equal to 0.4 A : we still get 440 x 0.4 = 176 At
We see that in this case, the transformer divides by five the value of the voltage from 220 to 44 V, but raises in the same ratio the intensity of the current, by multiplying by 5 and thus carrying it 0.4 at 2 amperes.
We thus find that, while the primary and secondary voltages are all the greater as the number of turns of the corresponding windings is higher, on the contrary, the currents are even lower than the number of turns of the same. windings is bigger.
To understand it, it is necessary to examine the electric power put into play in the transformer.
The secondary power is obtained by multiplying the voltage supplied to the secondary by the current flowing in this winding ; for example, for the transformer of Figure 6-a, this power is 440 x 2 = 880 W.
By multiplying the voltage applied to the primary current flowing in this winding is obtained, on the contrary, the primary power, which is therefore 220 x 4 = 880 W for the same transformer of Figure 6-a.
Similarly, for the transformer of Figure 6-b, the secondary power is 44 x 2 = 88 W, and the primary power is 220 x 0.4 = 88 W.
We thus see that, in the case of a step-up transformer, as in that of a step-down transformer, the power supplied by the secondary to the load is equal to that supplied by the network to the primary : this means that the transformer is only transporting the power required for the load connected to it from primary to secondary, while varying the values of the voltage and current on which this power depends.
In reality, the power supplied by the network to the transformer is always a little higher than that which is necessary for the load because part of this power is lost in the transformer ; we will see how power losses can occur in the transformer.
 1. 4. - LOSS OF POWER IN THE TRANSFORMER
1. 4. - LOSS OF POWER IN THE TRANSFORMER
Power losses occur in the windings and in the core of the transformer.
The power lost in the windings is due to the resistance of the conductor which constitutes them, resistance giving rise to voltage drops which are no longer negligible when the transformer, operating in charge, is traversed by currents more intense than when it operates empty.
The effect of these voltage drops produced in the windings consists of a reduction of the secondary voltage, a reduction which can be prevented by winding at the secondary a number of turns slightly higher than that which is necessary to obtain the desired transformation ratio. In this way, when the transformer runs empty, a secondary voltage is obtained which is a little higher than the value one should have, but which drops to this exact value when the transformer is operating under load, precisely because of voltage drops.
The power lost in the windings dissipates in the form of heat, determining an increase in the temperature of the windings, with the risk of deteriorating their insulation.
It must be remembered that the turns, wound on several superimposed layers, are isolated from each other by the enamel covering the wires and that the layers are isolated from each other by strips of waxed paper.
It is immediately understood that the enamel and wax paper can deteriorate if the driver reaches an excessive temperature, thus causing short circuits between the turns and rendering the windings unusable. To avoid this, conductors of a section appropriate to the current that should travel through them should be used so as not to have excessive power dissipations and dangerous temperature increases.
The section of the conductors is determined from the maximum allowable current density, that is, from the maximum current that can pass through each square millimeter of their section without raising the temperature to dangerous values.
The most suitable current density is often given by the results obtained in practice.
For the transformers we are seeing, it has been found that the current density should not exceed 3 A for every square millimeter of the section. This means that if a winding is to be traversed by a current of 3 A, the conductor who constitutes it must have a section of 1 mm2 ; if, on the contrary, the winding is to be traversed by a current of 6 A, the conductor must have a section of 2 mm2, so that on each square millimeter there is always only 3 A ; if the current is only 1.5 A, it is sufficient that the driver has a section of 0.5 mm2.
The density of the current is indicated by the Greek letter i (iota) and is measured in amperes per square meter (symbol A / m2). In practice, it is inconvenient to measure the small sections of the conductors in square meters and so we use the square millimeter, as we saw above ; the density of the current is thus generally expressed in amperes per square millimeter (symbol A / mm2).
All this allows us to understand why, when using a transformer, care must be taken not to connect to its secondary a load requiring a current higher than the maximum current that can provide the winding, so as not to exceed in the drivers the maximum current density and do not risk damaging the transformer.
Normally, the transformer manufacturer indicates the load current and the secondary power usually expressed in volt-amperes (symbol VA), that is the product of the volts by the amps of the secondary.
Now let's look at the power losses that occur in the transformer core.
We must first observe that, just as the primary induces a current in the secondary, so it induces a current in the core (the latter being of a ferromagnetic material, is also a conductor). These currents are called currents FOUCAULT, the name of the French Leon FOUCAULT (1819 - 1868) who, first, demonstrated experimentally existence.
When circulating in the core, FOUCAULT currents dissipate electrical power that must be considered lost because it can not be transported from primary to secondary.
It is necessary to know that they circulate in the different spaces of the core according to the routes indicated by the dotted lines of Figure 7-a.
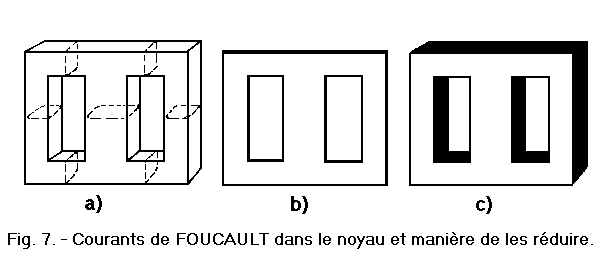
So that the currents do not follow these paths, the nucleus is not made of a single solid block, but of numerous sheets of very thin sheet, which all have the form indicated by the Figure 7-b ; one side of the sheets is insulated by a sheet of paper or, more often, by a layer of varnish. The sheets are joined together, as in Figure 7-c, in sufficient number to form the core of the desired thickness.
In this way, the currents can no longer follow the path indicated by Figure 7-a, because between two sheets, they meet the insulating layer ; so they circulate in each sheet, but given their very thin, they meet a very important resistance that significantly reduces their intensity. Moreover, we do not build the sheets with pure iron, but with iron mixed with a little silicon, which further increases their resistance, thus reducing to low values the currents of FOUCAULT and the losses they occur.
In addition to these losses, there are also hysteresis losses in the nucleus. As we have seen in the previous lesson (13. 2. Magnetic circuits), the phenomenon of magnetic hysteresis consists in a certain delay of the small elementary magnets to follow, by their orientation, the variations of the alternating current ; this delay is indicative of a certain "laziness" of small magnets to orientate themselves, "laziness" which must be overcome at the expense of an electric power that must be considered as lost, because it can not be transported to the secondary level and used by the load.
 1. 5. - CORE SECTION
1. 5. - CORE SECTION
As far as the kernel is concerned, we still have to see how we can determine the flow of induction passing through it.
From what was said in the previous lesson about magnetic circuits, we know why the flux through the core can be compared to the current flowing in an electrical circuit.
We have previously examined the density of the current ; for the nucleus, we must now see the density of flux, more often called induction, that is, the flux that passes through every square centimeter of the core section.
This section of the nucleus is examined from that, drawn in black in Figure 8, which is traversed perpendicularly by the induction lines of the whole flux.
Induction is indicated by the letter B and measured in webers per square meter (symbol Wb / m2) also called tesla (symbol T).
We have seen the density of the current to limit the temperature of the conductors to non-dangerous values ; we need to see the density of the flow to prevent kernel saturation from occurring.
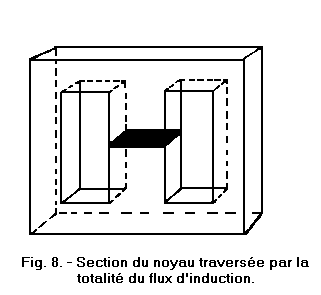
Indeed, if the induction reaches too high values, that is to say if every square centimeter of the section of the core is crossed by an excessive flux, the core saturates because all its small magnets are then oriented : the flow can not increase significantly, even if the current that produces it always increases. This should be avoided because, in order for the operation of the transformer to be correct, the flux must always vary at the same time as the current.
Induction values are also found experimentally : induction is generally assigned a maximum value between 1 and 1.3 teslas.
If we know the induction, that is to say the flow that passes through each square meter, or better, each square centimeter of the section of the core and if we also know the surface of this section, we can determine the maximum flux, multiplying the induction by the section.
To find the section of the kernel, one can also resort to the practice, which made it possible to note that one could calculate this section (S) by extracting the square root of the power (P) of the transformer and by multiplying the number obtained by 1.1.

Thus, the induction flux depends on the power of the transformer and this justifies the process of which we have spoken, because the power transfer from primary to secondary occurs precisely via the induction flux embraced by the two windings, and we understand that this flow must be all the greater as this power is greater.
For a 100 VA transformer, there is a section of :

 2. - AUTOTRANSFORMERS
2. - AUTOTRANSFORMERS
As we have seen, the transformer operates according to the phenomenon of mutual induction which occurs between the two windings ; but, in the preceding lessons, we have also seen the analogous phenomenon of self-induction which occurs in a single winding. By exploiting this last phenomenon, a device similar to the transformer has been realized and which nevertheless comprises only one winding in place of the primary and the secondary.
This device is called an autotransformer and, like the transformer, it can be either an elevator or a step-down.
To better understand how the autotransformer works, we first have to look at the voltage-reducing autotransformer which, as shown in Figure 9-a, consists of a core (of the same type as that used for the transformers) around which is arranged the winding, provided with an intermediate socket indicated by B and a second socket connected to the end A.
In Figure 9-b is drawn the graphic symbol which is used to represent the autotransformer in the electrical diagrams and we see how this element is connected to the sector and the load.
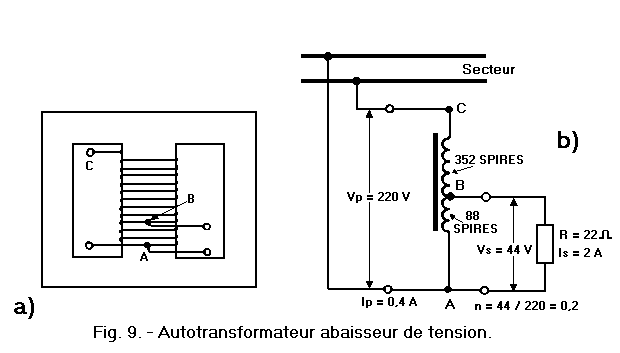
Since the winding comprises 352 + 88 = 440 turns, if we suppose that the flux embraced by these turns induces in each of them a f.e.m. 0.5 V, between the ends A and C a f.e.m. 440 x 0.5 = 220 V, equal to the mains voltage applied between these ends.
If in each turn, 0.5 V is induced, at the ends of the 88 turns between the end A and the intermediate tap B, induces a f.e.m. 88 x 0.5 = 44 V, thanks to which a current of 2 amperes can be circulated in the 22 ohm resistor.
So we see that with the autotransformer, we can reduce the mains voltage five times, from 220 to 44 V, as was done with the transformer of Figure 6-b.
The voltage of the load is thus obtained on a part of the same winding to which the mains voltage is applied : the 440 turns between A and C, between which the mains voltage is applied, can therefore be considered as primary turns, while that the 88 turns between the end A and the tap B, where the voltage of the load is obtained, can be considered as secondary turns.
Thus, between the number of its primary and secondary turns and between the currents and the corresponding voltages, the relations we found for the transformers are valid. In particular, we will call transformation ratio of the autotransformer, the number obtained by dividing the voltage delivered by the secondary by the voltage applied to the primary.
The only difference with the transformer consists in the fact that some primary turns also serve as secondary turns and are therefore traversed by the primary current and the secondary current.
Let us now consider the autotransformer voltage booster, whose constitution is shown in Figure 10-a, while in Figure 10-b, we can see how the ends A and C of the winding and the intermediate socket B are connected to the sector and to the load.
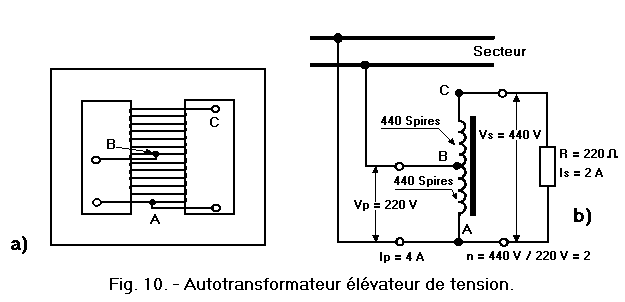
In this case, the mains voltage is applied to the 440 turns between the end A and the B tap, assuming that the flux induces in each of these turns a f.e.m. 0.5 V, between these points a f.e.m. 440 x 0.5 = 220 V, precisely equal to the mains voltage.
We must observe that the induction lines, by closing through the nucleus, embrace the entire coil arranged around it and thus the other 440 turns between the B-tap and the C-end : in each of these turns one fem 0.5 V is thus induced, and between these points, we thus obtain a f.e.m. 440 x 0.5 = 220 volts.
Between the ends A and C of the winding, we thus obtain a f.e.m. 220 + 220 = 440 V, which allows to circulate the current of 2 A in the resistance of 220 Ω connected to these same ends.
We see that with this autotransformer, we can double the mains voltage of 220 to 440 V, as is done with the transformer of Figure 6-a.
The voltage of the sector is now applied to a part of this winding from which the voltage of the load is obtained : the 880 turns between the ends A and C, where the voltage of the load is obtained, can therefore be considered as secondary turns, while the 440 turns between the end A and the tap B to which the mains voltage is applied can be considered as primary turns.
Thus, for the step-up autotransformer, it can be said that between the number of primary and secondary turns and between the corresponding voltages and currents, the same relations as those found for the transformer apply ; in this case, we can also call the conversion ratio of the autotransformer the number obtained by dividing the voltage delivered by the secondary by the voltage applied to the primary.
The only difference with respect to the transformer consists in the fact that certain secondary turns also serve as primary turns and are therefore traversed by the primary current and the secondary current.
For the voltage-boosting autotransformer, the fact already seen for the voltage-reducing autotransformer is thus verified, that is to say that, in the winding portion between the intermediate tap B and the end A, circulate the primary current and the secondary current.
These two currents behave as we have already seen for the transformer, producing two f.m.m. and therefore two equal and opposite induction flows; for this, the currents must flow in the opposite direction, that is, while one is directed, for example, from the intermediate tap B to the end A, the other is directed from the end A to socket B and vice versa.
In fact, in the winding portion between the tap B and the end A circulates a current equal to the difference between the primary and secondary currents ; if these currents have a slightly different intensity, the current which results from their difference has a reduced intensity.
This winding part can therefore be made with a conductor of a smaller section than the rest of the winding; it is thus traversed by a current of reduced intensity which gives rise to a lower power dissipation.
We also see that the autotransformer does not have a secondary winding, and we can conclude that this device has a smaller volume, lighter and less expensive than a transformer of equal power. In addition, an autotransformer also saves part of the ferromagnetic material required for its core.
Indeed, the power that a transformer provides to the load must be fully transported from the primary circuit to the secondary circuit through the induction flow, because it is the only element that these two circuits have in common.
In the case of the autotransformer, on the other hand, these two circuits also have in common the winding portion between the tap B and the end A, and also the power relative to this space, which is not necessary. transform by varying the voltage and consequently the current.
The autotransformer effectively transforms only the power relative to the winding portion between the tap B and the end C, by transferring it, via the induction flux, to the winding part. between socket B and end A, to which the load is connected.
This power is also called transformed power and is calculated by multiplying the voltage that exists between the points B and C by the current flowing through the winding space between these points.
For example, for the autotransformer of Figure 9, a voltage of 220 - 44 = 176 V is obtained between B and C, whereas the intensity of the current is 0.4 A, and the transformed power is therefore : 176 x 0.4 = 70.4 W.
Since the load requires a power of 44 x 2 = 88 W, this means that the power of 88 - 70.4 = 17.6 Watts goes directly from primary to secondary.
So we see that, while in the case of a transformer, it would have been necessary to calculate the section of the core according to the total power of 88 W, we can calculate the section of the core of the autotransformer according to the transformed power which is only 70.4 W, so the kernel is of smaller dimensions, even if it is of little.
We could obtain a larger reduction of the dimensions of the core of the autotransformer of Figure 10 : Indeed, since between B and C we have the voltage of 440 - 220 = 220 V, with a current of intensity of 2 A, the transformed power is 220 x 2 = 440 W, that is to say half of the total power demanded by the load, which is 440 x 2 = 880 W.
These examples show us that the transformed power decreases with respect to the total power demanded by the load when the turns between the tap B and the end A increase relative to those of the entire winding. Indeed, while on the autotransformer of Figure 9, the turns between these two points form only the fifth of the turns of the entire winding, on the autotransformer of Figure 10, the turns between these points form on the contrary, half of the turns of the entire winding.
Increasing the turns between the points A and B relative to those of the entire winding therefore has the advantage of reducing the size of the core as a result of the decrease in the transformed power. Moreover, as we have seen above, the turns between the points A and B are wound with a conductor of small section, and when they increase, we obtain a greater economy of the material not only in the construction of the core, but also in the execution of the winding.
Finally, we observe that, if we increase the turns between A and B with respect to all the turns, the difference between the primary voltage and the secondary voltage decreases, that is to say that the transformation ratio is getting closer and closer to 1 ; this ratio would be equal to 1 if the primary voltage was equal to the secondary voltage.
We can therefore conclude that the autotransformer is all the more advantageous compared to the transformer that its transformation ratio is closer to 1.
But the autotransformer also has a disadvantage compared to the transformer ; this can be seen by examining Figure 11 where these two elements are shown connected to the sector via a switch.
As seen in Figure 11-a, the secondary circuit of the transformer is not connected to the mains ; it is therefore not energized when the switch is opened to interrupt its operation.
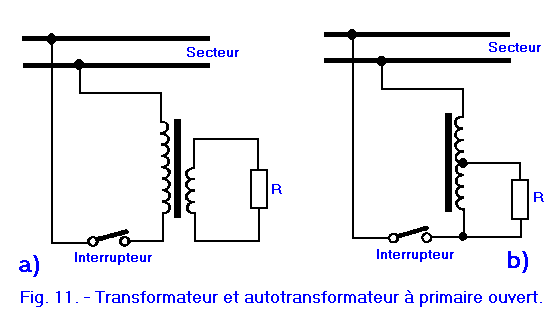
In contrast, the secondary circuit of the autotransformer (Figure 11-b) is connected to the sector through the winding ; when the switch is opened, the circuit remains connected to one of the mains conductors and is therefore energized.
When the autotransformer feeds a device, all these circuits are mounted on a metal frame to which is generally connected one end of the autotransformer.
The chassis is powered up and, if touched, it can receive an electric shock even when the device is off. In this case, to avoid unpleasant jolts, unplug the power plug before touching the chassis.
So far, we've seen resistors, capacitors, windings, transformers, and autotransformers, that is, fundamental passive components.
In the next theory, we will introduce a special chapter of a general nature : electrical measurements, which concern all fields of electronics.



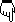 Vacuum operation of the transformer
Vacuum operation of the transformer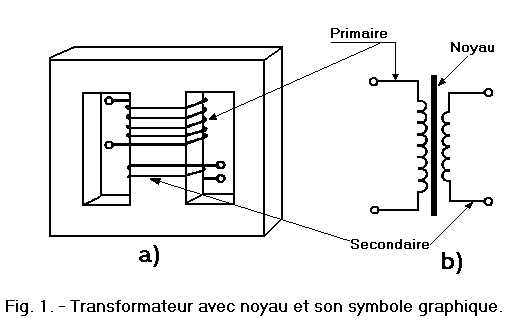









 Click here for the next lesson or in the summary provided for this purpose.
Click here for the next lesson or in the summary provided for this purpose. Next Page
Next Page