Formules et le Calcul Littéral :
MATHÉMATIQUES "1ère Partie"
Dans cette leçon, nous allons traiter de quelques notions simples de mathématiques.
Il ne s'agit pas d'un cours de mathématiques proprement dit, ce qui n'est pas notre but, mais de l'exposer des connaissances nécessaires à la bonne compréhension des différentes théories traitant de l'étude des circuits électroniques sans oublier l'informatiques.
Nous considérons que les opérations élémentaires d'arithmétique sont connues, c'est-à-dire l'addition, la soustraction, la multiplication et la division.
L'esprit avec lequel seront traitées ces mathématiques ayant été précisé, nous allons vous présenter le contenu de notre première théorie.
Le premier paragraphe est consacré aux formules. Qu'est-ce qu'une formule, comment la lire, comment s'en servir, c'est ce que nous apprendrons. Cela nous amènera tout naturellement au calcul littéral qui fait l'objet du second paragraphe.
Nous compléterons nos connaissances d'arithmétique par l'étude d'une nouvelle opération : l'élévation à une puissance, à laquelle le troisième paragraphe est consacré. L'opération inverse, c'est-à-dire l'extraction de racine sera traitée dans le quatrième.
Le cinquième, quant à lui, nous rappellera (ou nous apprendra) ce que sont les fractions, comment les simplifier, les additionner, les soustraire, les multiplier...
Le sixième, quant à lui, nous verrons qu'une fraction peut parfois s'appeler un rapport. Enfin, toujours dans le même esprit de fractions ou de rapports, le septième et dernier paragraphe nous apprendra à manipuler les proportions.
Dans votre intérêt, nous vous invitons à effectuer les exemples donnés, non pas seulement le jour de la lecture, mais aussi bien après celle-ci (plusieurs jours, semaines ou mois. En mathématiques, comme et beaucoup d'autres matières, rien ne vaut la pratique et la répétition pour bien comprendre et retenir.
1. - LES FORMULES
L'usage des abréviations s'est très répandu. De nombreuses administrations, organisations industrielles, commerciales ou politiques, se font connaître par des sigles formés de quelques lettres que le public garde facilement en mémoire, même s'il oublie souvent leur signification exacte (SNCF, ERDF-GRDF, CNRS. L'habitude des abréviations est entré depuis très longtemps dans le domaine des sciences mathématiques, chimiques et physiques. Cela donne un degré de concision très élevé aux descriptions scientifiques ce qui est un avantage appréciable pour l'exactitude des calculs effectués.
Voyons par quelles lettres il a été convenu de représenter certaines grandeurs électriques :
Différence de potentiel, tension électrique : V ou U
Capacité électrique : C
Intensité du courant électrique : I
Résistance électrique : R
Quantité d'électricité : Q
Résistivité : p (prononcer "RHÔ"), lettre R de l'alphabet grec)
Les abréviations de ce type sont à la base de toutes les simplifications qu'il convient d'exécuter pour obtenir des expressions mathématiques. La méthode peut être étendue à la représentation de toutes les grandeurs apparaissant dans l'étude des phénomènes, à condition de toujours préciser la signification de chaque lettre, et de veiller ensuite, à n'utiliser chacune de celles-ci que pour indiquer la grandeur correspondante.
Par conséquent, si nous avons établi par exemple que les lettres V, I et R représentent respectivement la tension, l'intensité du courant et la résistance d'un circuit électrique, nous ne pourrons pas, par la suite, attribuer à ces mêmes lettres une autre signification ou exprimer ces mêmes grandeurs par des lettres différentes.
Chaque lettre de l'expression mathématique représente non seulement un type donné de grandeur, mais aussi toutes les valeurs possibles de cette grandeur. Par exemple la lettre V, utilisée pour indiquer la tension, peut signifier 1 volt, 25 volts, 220 volts... c'est-à-dire toutes les valeurs de tension possibles. De façon analogue, la lettre I utilisée pour indiquer l'intensité du courant, peut signifier 0,5 ampère, 2 ampères, 5 ampères... De même, la lettre R représentant la résistance du circuit peut signifier 3 ohms, 100 ohms, 10 000 ohms...
Cette règle est valable pour toute autre lettre utilisée dans une expression mathématique. On retrouve également des nombres qui restent inchangés lorsque l'on assigne successivement aux lettres toutes les valeurs possibles. Ces nombres sont appelés coefficients.
Il est évident que l'absence de tout signe ne peut se justifier lorsque, aucune confusion n'est possible, (c'est-à-dire +, -, x, :, / etc...), c'est le cas du calcul littéral dont il est question plus loin.
![]() 1. 2. - ÉTABLISSEMENT
D'UNE FORMULE
1. 2. - ÉTABLISSEMENT
D'UNE FORMULE
Voyons maintenant comment on obtient la simplification mathématique de l'énoncé d'une loi physique en prenant comme exemple : la loi d'Ohm.
La loi d'Ohm est exprimée dans les formes suivantes :
-
Lorsque la tension augmente, l'intensité du courant augmente ;
-
On obtient la résistance en divisant la tension par l'intensité ;
-
On obtient la tension en multipliant la résistance par l'intensité ;
-
On obtient l'intensité en divisant la tension par la résistance.
La première forme de l'énoncé (de couleur rouge) est purement descriptive et ne peut être traduite par une expression mathématique parce qu'elle ne précise pas dans quelle mesure l'intensité augmente lorsque la tension appliquée au circuit augmente. Au contraire, les trois expressions suivantes se prêtent à une traduction mathématique complète.
Voici comment on procède dans chaque cas :
1 - On obtient la résistance en divisant la tension par l'intensité.
On peut donc écrire : Résistance = Tension / Intensité
Cela est le premier pas et aussi le plus important que l'on vient d'accomplir pour arriver à l'expression mathématique. Le suivant consiste simplement à remplacer les mots par des lettres. Si nous convenons de représenter la résistance par la lettre R, la tension par la lettre V et l'intensité par la lettre I, nous pouvons exprimer la relation précédente de la façon suivante :
R = V / I
Avec ce résultat, nous avons obtenu la simplification la plus poussée de la première partie de l'énoncé, en mettant bien en évidence l'opération qu'il faut exécuter pour obtenir la valeur de la résistance d'un circuit en connaissant les valeurs de la tension et de l'intensité.
Les expressions de ce genre, qui contiennent des lettres (remplaçant les noms de grandeurs données), des symboles d'opérations (à effectuer avec les valeurs des grandeurs) et le symbole de l'égalité (qui exprime le lien existant entre une grandeur et les autres) sont appelées des formules mathématiques ou expressions littérales ou plus simplement formules.
Lorsque la formule est obtenue, il suffit de s'en souvenir ainsi que de la signification exacte des lettres afin de pouvoir l'utiliser dans les calculs.
L'application de la formule est très facile : il suffit de remplacer les lettres par les valeurs connues des grandeurs et d'exécuter les calculs.
Prenons un exemple : Un circuit auquel on applique une tension (V) de 15 volts est parcouru par un courant d'intensité (I) de 3 ampères ; calculez d'après ces données, la résistance (R) de ce circuit.
Pour effectuer ce calcul d'une façon ordonnée, il convient d'écrire d'abord la formule et ensuite, sous cette dernière, l'expression que l'on obtient en remplaçant les lettres par leur valeur respective :
R = V / I
R = 15 / 3 = 5 Ohms
D'où R = 5 Ohms
Le nombre 5 qui a été obtenu en effectuant la division 15 / 3, représente la valeur de la résistance R.
En conclusion du calcul effectué en fonction de la loi d'Ohm, on peut affirmer qu'un circuit, auquel on applique une tension de 15 volts et dans lequel passe un courant d'une intensité de 3 ampères, doit avoir une résistance de 5 Ohms.
Essayons maintenant d'interpréter par le même procédé, l'énoncé suivant :
2 - On obtient la tension en multipliant la résistance par l'intensité.
En reprenant la simplification, on peut écrire :
Tension = Résistance x Intensité
Et en conservant aux lettres la même signification qu'auparavant, nous obtenons la formule suivante :
V = R x I
L'application de cette formule est tout aussi simple que la précédente.
Exemple : Un circuit ayant une résistance (R) de 5 Ohms est parcouru par un courant d'une intensité (I) de 3 ampères ; calculez la valeur de la tension (V) appliquée à ce circuit :
On aura : V = R x I soit V = 5 x 3 = 15 volts.
La tension appliquée au circuit est de 15 volts.
Traduisons maintenant le dernier énoncé de la loi d'Ohm en le mettant en formule :
3 - On obtient l'intensité en divisant la tension par la résistance.
On peut donc écrire : Intensité = Tension / Résistance et en remplaçant les mots par les lettres correspondantes :
I = V / R
Exemple : On applique à un circuit, ayant une résistance (R) de 5 Ohms et une tension (V) de 15 volts ; calculez l'intensité du courant (I) absorbé par ce circuit :
Nous savons que : I = V / R
d'où I = 15 / 5 = 3 ampères
L'intensité du courant absorbé par le circuit est donc de 3 ampères.
Comparons maintenant les trois formules obtenues à partir des énoncés de la loi d'Ohm :
-
La première R = V / I, représente une division de la tension par l'intensité dont le résultat donne une valeur de résistance ;
-
La deuxième V = R x I, représente une multiplication de la résistance par l'intensité dont le résultat donne une valeur de tension ;
-
La troisième I = V / R, représente une division de la tension par la résistance dont le résultat est une valeur d'intensité.
Puisqu'il existe trois formules distinctes, nous pourrions être amenés à penser qu'il existe trois lois d'Ohm, cette conclusion serait erronée. En réalité, les trois formules sont équivalentes entre elles car elles représentent trois aspects d'un même lien.
Cette affirmation peut être facilement démontrée à l'aide d'exemples choisis au hasard, qui montrent que toutes les valeurs qui satisfont une seule des trois formules, satisfont également les deux autres.
Dans les trois exemples ci-dessus, nous avons déjà trouvé que les valeurs de 15 volts, 3 ampères et 5 ohms, répondent de façon satisfaisante aux formules R = V / I ; V = R x I et I = V / R.
Considérons maintenant un autre exemple choisi au hasard.
Un circuit ayant une résistance (R) de 150 ohms est parcouru par un courant d'une intensité (I) de 2 ampères ; calculez la valeur de la tension (V) appliquée à ce circuit.
Pour calculer la valeur de la tension, il faut choisir entre les trois formules, celle qui présente, à gauche du signe = la lettre V, qui représente la tension. On voit immédiatement que la seconde formule est celle qui convient ; donc, en suivant la procédure habituelle, nous aurons :
V = R x I
V = 150 x 2 = 300 volts
La tension appliquée au circuit est donc de 300 volts. Nous pouvons maintenant nous assurer que ces mêmes valeurs de 150 ohms, 2 ampères et 300 volts répondent également aux deux autres formules de la loi d'Ohm.
En utilisant la première formule, nous obtenons, en effet :
R = V / I
R = 300 / 2 = 150 ohms
Le résultat de 150 ohms est exactement celui que nous attendions pour une tension de 300 volts et une intensité de 2 ampères, sur la base des calculs précédents.
En utilisant la troisième formule, nous obtenons :
I = V / R
I = 300 / 150 = 2 ampères
Ce résultat de 2 ampères est aussi celui obtenu précédemment.
On pourrait prendre de nombreux exemples semblables à celui-ci.
Chacun d'eux démontrerait toujours que les trois valeurs : tension, intensité et résistance d'un circuit, répondent de façon satisfaisante aux trois formules. Vous pouvez alors vous demander à quoi servent trois formules équivalentes, dérivées de la loi d'Ohm, liant entre elles les mêmes valeurs. Une seule formule ne suffirait-elle pas ? Non, parce que chacune d'elles permet d'effectuer rapidement un calcul bien déterminé :
-
Avec la première formule (R = V / I), nous pouvons calculer la valeur de la résistance lorsque celles de la tension et de l'intensité sont données ;
-
Avec la deuxième formule (V = R x I), nous pouvons calculer la valeur de la tension en connaissant les valeurs de la résistance et de l'intensité.
-
Avec la troisième formule (I = V / R), nous pouvons calculer la valeur de l'intensité en connaissant celles de la tension et de la résistance.
Il est intéressant de noter que le nombre de formules équivalentes obtenues à partir de la loi d'Ohm, est de trois, de même qu'il apparaît trois lettres différentes dans les formules correspondant aux trois grandeurs caractéristiques du circuit (tension, intensité, résistance).
Cette concordance de nombres n'est pas le fait du hasard.
Si le nombre des grandeurs liées entre elles était trois, quatre ou cinq..., nous obtiendrions respectivement des formules contenant trois, quatre ou cinq lettres et un même nombre de formules équivalentes, toutes également aptes à exprimer complètement le lien entre les grandeurs considérées.
Si, pour toutes les lois de l'électronique, nous devions suivre la même procédure que nous avons adoptée pour la loi d'Ohm, nous obtiendrions une quantité invraisemblable de formules, ce qui en rendrait l'étude excessivement longue et ardue.
On est donc amené à se poser une question : est-il vraiment nécessaire de tirer toutes les formules équivalentes d'une loi, puisqu'elles signifient toutes la même chose ?
La réponse est assez rassurante : il n'est pas nécessaire de tirer directement de l'énoncé d'une loi toutes les formules équivalentes : il suffit d'en tirer une seule, quelle qu'elle soit, et à partir de celle-ci, on pourra ensuite reconstituer toutes les autres, au moyen des règles simples du calcul mathématique.
Dans cette perspective, nous allons maintenant établir quelques unes des règles simples qui nous permettront de passer d'une formule donnée à une autre.
![]() 2. - LE CALCUL
LITTÉRAL
2. - LE CALCUL
LITTÉRAL
2. 1. - RÈGLES
Pour nous préparer aux règles qui permettent de passer rapidement et sans peine d'une formule à l'autre, considérons sous un angle différent les trois formules de la loi d'Ohm.
En premier lieu, convenons d'appeler premier membre, la partie de la formule qui se trouve à gauche du signe =, et second membre, la partie qui se trouve à sa droite.
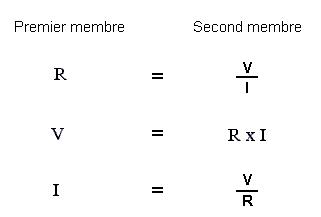
Cette convention est valable pour toute expression mathématique constituée de deux parties liées entre elles par la relation d'égalité. Lorsque le signe = apparaît dans une expression mathématique, celle-ci s'appelle égalité, et la règle suivante est toujours valable :
Règle 1 : Si l'on intervertit entre eux les 2 membres d'une égalité, on obtient une nouvelle égalité équivalente à la première.
En nous basant sur cette règle, nous pourrons écrire indifféremment :
R = V / I ou V / I = R
V = R x I ou R x I = V
I = V / R ou V / R = I
En effet, si nous considérons les valeurs correspondant aux lettres (15 volts, 3 ampères et 5 ohms) qui ont été trouvées au cours des trois premiers exercices, nous ne trouvons aucune différence entre :
5 = 15 / 3 ou 15 / 3 = 5
15 = 5 x 3 ou 5 x 3 = 15
3 = 15 / 5 ou 15 / 5 = 3
Lorsqu'une expression mathématique et en particulier une formule contiendra une multiplication, nous pourrons appliquer la règle suivante :
Règle 2 : On ne change pas la valeur d'une multiplication, si l'on intervertit l'ordre des facteurs.
En combinant cette règle à la précédente, nous pouvons écrire par exemple, la deuxième formule de la loi d'Ohm des quatre façons suivantes, toutes également correctes :
|
V = RI |
ou |
V = IR |
ou |
RI = V |
ou |
IR = V |
En effet, en reprenant le précédent exemple numérique, on trouve que les valeurs admissibles dans la première des quatre formules indiquées ici, le sont également pour les trois autres :
|
15 = 5 x 3 |
ou |
15 = 3 x 5 |
ou |
5 x 3 = 15 |
ou |
3 x 5 = 15 |
Jusqu'ici nous avons considéré l'aspect des formules en changeant les lettres de place sans en changer les valeurs. Maintenant, nous allons faire quelque chose de plus : en nous basant sur quelques autres règles, nous changerons les valeurs en conservant toutefois l'égalité entre le premier et le second membre.
Règle 3 : Si l'on multiplie les deux membres d'une égalité par un même nombre, on conserve l'égalité.
Considérons la première forme de la loi d'Ohm.
Multiplions le premier et le second membre de la formule R = V / I par un même nombre, par exemple 7, et, reprenons notre circuit avec la valeur R soit 150 ohms, celle de V de 300 volts et celle de I de 2 ampères ; nous aurons :
R x 7 = V / I x 7
150 x 7 = 300 / 2 x 7
1050 = 150 x 7
1050 = 1050
Le résultat nous indique de façon évidente que malgré la multiplication effectuée, les deux membres restent toujours égaux entre eux.
Règle 4 : Si on divise les deux membres d'une égalité par un même nombre, on conserve l'égalité.
Considérons la seconde formule de la loi d'Ohm : V = RI. Prenons les mêmes valeurs que dans l'exemple précédent et divisons chaque terme par 50 :
V / 50 = R x I / 50
300 / 50 = 150 x 2 / 50
6 = 300 / 50
6 = 6
Ce résultat démontre que malgré les divisions effectuées, les deux membres restent toujours égaux entre eux.
Dans les deux exemples précédents, on a choisi au hasard les nombres 7 et 50, mais n'importe quel nombre pourrait servir à démontrer l'exactitude des règles trois et quatre.
Voici maintenant deux autres règles permettant de passer rapidement d'une formule donnée à ses équivalentes :
Règles 5 : Si un membre d'une égalité est constitué par une division, le diviseur peut être transféré à l'autre membre comme facteur de multiplication.
Prenons la troisième forme de la loi d'Ohm, soit I = V / R. En nous basant sur la règle qui vient d'être énoncée, on obtient :
I x R = V
Exemple : Dans un circuit la valeur de la tension (V) est égale à 60 volts et celle de la résistance (R) à 15 ohms. L'intensité (I) que l'on obtient en divisant 60 par 15, a pour valeur :
I = V / R
4 = 60 / 15
4 = 4
Faisons passer maintenant R (diviseur dans le 2ème membre) dans le premier membre comme multiplicateur. Nous avons :
I x R = V
4 x 15 = 60
60 = 60
Ces deux résultats démontrent qu'en passant de la première forme à la seconde, on conserve l'égalité.
Règle 6 : Si un membre d'une égalité est constitué par une multiplication, l'un des facteurs quel qu'il soit peut être transféré à l'autre membre comme diviseur.
Exemple :
|
1 ) V = R x I |
2 ) V / I = R |
3 ) V / R = I |
|
60 = 15 x 4 |
60 / 4 = 15 |
60 / 15 = 4 |
|
60 = 60 |
15 = 15 |
4 = 4 |
Les trois résultats démontrent que l'on a conservé l'égalité des deux membres en passant d'une forme à l'autre.
Les opérations au moyen desquelles on peut transférer dans une expression mathématique une lettre d'un emplacement à un autre, en conservant l'égalité des deux membres, prennent le nom de calcul littéral (ou calcul algébrique), par analogie avec le nom de calcul numérique (ou calcul arithmétique) que l'on a donné aux opérations effectuées avec des nombres.
Nous allons maintenant préciser les notions qui ont été exposées ici, au moyen d'un exemple d'application du calcul littéral au domaine de l'électronique.
![]() 2. 2. - APPLICATION
DU CALCUL LITTÉRAL
2. 2. - APPLICATION
DU CALCUL LITTÉRAL
Nous verrons que la résistance électrique d'un conducteur dépend de sa longueur, de sa section et de sa résistivité. (La résistivité est une caractéristique du matériau constituant le conducteur).
Si nous voulons traduire en formules mathématiques cet énoncé, nous nous trouvons extrêmement embarrassé. En effet, il n'est pas précisé de quelle quantité la résistance du conducteur varie quand on augmente ou on diminue la longueur, la section ou la résistivité. Pour surmonter cette obstacle, il faut se référer à un énoncé plus précis, tel que : on obtient la résistance d'un conducteur en multipliant sa résistivité par sa longueur et en divisant le produit obtenu par sa section.
Cet énoncé peut être abrégé de la manière suivante :

Convenons de représenter la résistance par la lettre R, la résistivité par la lettre grecque r , la longueur du conducteur par la lettre minuscule l, et sa section par la lettre majuscule S, nous obtenons la formule suivante :
R = r x l / S
Au moyen de cette formule, nous pouvons alors calculer la résistance d'un conducteur quelconque, connaissant sa longueur, sa section et sa résistivité.
Si la résistivité est exprimée au moyen de l'unité de mesure ohm-centimètre, la longueur en centimètres et la section en centimètre carrés, la valeur de la résistance sera exprimée en ohms.
Exemple : Une barre cylindrique a une longueur (l) de 60 centimètres, une section (S) de 3 centimètres carrés et est constituée d'une matière ayant une résistivité (r ) de 2 ohms-centimètre ; calculez sa résistance (R).
R = r x l / S
R = 2 x 60 / 3 = 2 x 20 = 40 ohms
La résistance de la barre est de 40 ohms.
Jusqu'ici, la procédure est analogue à celle que nous avons suivie en étudiant la loi d'Ohm.
Toutefois, il reste à voir comment on doit procéder pour obtenir, à partir de la formule unique que l'on a trouvée, les autres formules équivalentes, soit :
-
- La formule qui permet de calculer la résistivité du matériau lorsque l'on connaît la résistance, la longueur et la section du conducteur ;
-
- La formule qui permet de calculer la longueur d'un conducteur de section, de résistivité et de résistance données ;
-
- La formule qui permet de calculer la section d'un conducteur de longueur, de résistivité et de résistance données.
Les formules équivalentes sont donc au nombre de quatre puisqu'il y a quatre grandeurs. Comme chaque grandeur est déterminée en fonction des trois autres :
![]() Une formule est directement obtenue à partir de l'énoncé,
Une formule est directement obtenue à partir de l'énoncé,
![]() Les trois autres sont obtenues à partir de cette dernière au moyen de simples opérations de calcul littéral.
Les trois autres sont obtenues à partir de cette dernière au moyen de simples opérations de calcul littéral.
Voici comment l'on procède :
Écrivons la formule connue :
R = r x l / S
et observons (en nous basant sur la règle 6), que nous pouvons transférer la lettre (r ) ou la lettre (l) dans le premier membre, et en nous basant sur la règle 5, nous pouvons porter dans le premier membre, la lettre S. Exécutons successivement les opérations nécessaires :
1) Portons d'abord la lettre S (diviseur) dans le premier membre (donc multiplicateur) :
R x S = r x l
Portons maintenant la lettre l (multiplicateur) dans le premier membre (donc diviseur).
R x S / l = r
L'expression obtenue : r = R x S / l est la première des trois formules équivalentes que nous cherchons à établir, c'est-à-dire la formule qui permet de calculer la résistivité en fonction des trois autres grandeurs.
Exemple : La longueur (l) d'un conducteur est de 30 cm, sa résistance (R) de 10 ohms et sa section (S) est de 3 cm2. Calculons la résistivité (r) de la matière dont est constitué le conducteur.
r = R x S / l
r = 10 x 3 / 30 = 30 / 30 = 1 ohm-centimètre
La résistivité est donc 1 ohm par centimètre.
2) - Portons maintenant dans le premier membre de notre formule de départ, d'abord la lettre (S) et ensuite la lettre r .
R x S = r x l
R x S / r = l
L'expression obtenue : l = R x S / r est la seconde des formules équivalentes cherchées, soit celle qui permet de calculer la longueur d'un conducteur en fonction des trois autres grandeurs.
Exemple : La résistivité (r ) d'un conducteur est 3 ohms-centimètre, sa résistance (R) est 45 ohms, sa section (S) est 1 centimètre carré ; calculez la longueur (l) de ce conducteur.
l = R x S / r
l = 45 x 1 / 3 = 15 cm.
La longueur du conducteur est donc de 15 centimètres.
3) - Il reste à trouver la dernière formule équivalente. En partant de notre formule de base, nous portons la lettre (S) du second membre dans le premier et ensuite la lettre (R) du premier membre dans le second.
R x S = r x l (formule de base)
S = r x l / R
L'expression obtenue : S = r x l / R est la troisième des formules équivalentes cherchées, c'est-à-dire, la formule qui permet de calculer la section d'un conducteur en fonction des trois autres grandeurs.
Exemple : La résistance (R) d'un conducteur est de 50 ohms, sa résistivité (r) est de 1 ohm-centimètre, sa longueur (l) est de 5 cm ; calculez la section (S) de ce conducteur :
S = r x l / R
S = 1 x 5 / 50 = 5 / 50 = 0,1 cm2
La section du conducteur est donc de 0,1 centimètre carré.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente |
 Page suivante Page suivante
|
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.
 Établissement d'une formule
Établissement d'une formule
