 Réalisation du Schéma de la Signalisation par inverseurs Réalisation du Schéma de la Signalisation par inverseurs |
 Réalisation du Schéma de la Signalisation au moyen de symboles électroniques Réalisation du Schéma de la Signalisation au moyen de symboles électroniques |
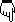 Bas de page Bas de page |
Exemple d'Application Pratique des Tableaux de Karnaugh :
4. - EXEMPLE D'APPLICATION PRATIQUE DES TABLEAUX DE KARNAUGH
4. 1. - Supposons que lorsque le réveil sonne le matin, on veuille savoir comment s'habiller avant même d'avoir ouvert les volets.
Nous disposons pour cela d'un dispositif adéquat placé à l'extérieur et comprenant notamment un thermomètre et un baromètre et qui nous donne les indications suivantes : temps chaud, temps doux, temps froid, temps pluvieux.
On décide que dans tous les cas, on mettra un pantalon, des chaussures et une chemise.
Il reste maintenant à déterminer s'il est nécessaire de mettre en plus une veste, un manteau, un imperméable ou de prendre un parapluie.
Nous appellerons les variables d'entrée :
![]() temps chaud : c
temps chaud : c
![]() temps doux :
d
temps doux :
d
![]() temps froid : f
temps froid : f
![]() temps pluvieux : p
temps pluvieux : p
Les variables de sortie seront matérialisées par des lampes et s'appellerons :
![]() veste
: V
veste
: V
![]() manteau : M
manteau : M
![]() imperméable : I
imperméable : I
![]() parapluie : P
parapluie : P
On admettra que lorsqu'il fait doux on met une veste, quand il fait froid on met une veste et un manteau et que lorsqu'il fait chaud, on ne met rien. Quand il pleut, on met un imperméable sur la veste sinon on prend un parapluie lorsque l'on a déjà un manteau ou lorsqu'il fait chaud.
A partir de ces postulats, établissons la table de vérité du système (figure 70).
Nous avons réservé une colonne qui correspond aux impossibilités. En effet, il ne peut faire chaud et froid par exemple.
Établissons les tableaux de Karnaugh que nous tirerons de la table de vérité et ce, pour chaque variable de sortie.
4. 2. - TABLEAU DE KARNAUGH RELATIF A LA VESTE (figure 71)
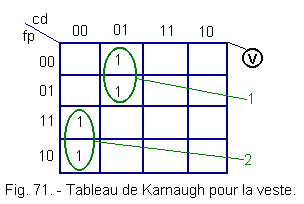
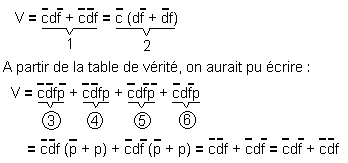
Ceci confirme le tableau de Karnaugh.
4. 3. - TABLEAU DE KARNAUGH RELATIF AU MANTEAU (figure 72)
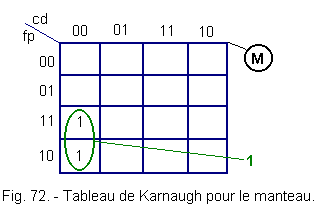

Ce qui confirme le tableau de Karnaugh.
4. 4. - TABLEAU DE KARNAUGH RELATIF A L'IMPERMÉABLE (figure 73)
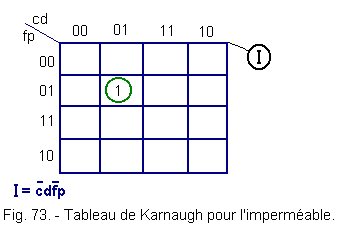
4. 5. - TABLEAU DE KARNAUGH RELATIF AU PARAPLUIE (figure 74)
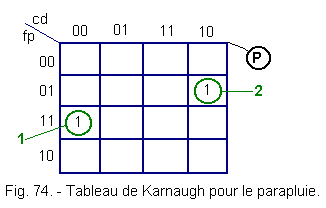
![]()
![]() 4. 6. - RÉALISATION DU SCHÉMA
DE LA SIGNALISATION PAR INVERSEURS
4. 6. - RÉALISATION DU SCHÉMA
DE LA SIGNALISATION PAR INVERSEURS
On utilisera des contacts inverseurs, qui seront commandés par le dispositif approprié évoqué précédemment, comme représentés figure 75.
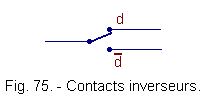
Dans l'exemple de la figure 75,
suivant la position de l'interrupteur, on a : d = 1
(high), d = 0 (low) soit
![]() ,
de telle sorte que d = doux et
,
de telle sorte que d = doux et ![]() = non doux.
= non doux.
![]() a) - Schéma pour la veste (figure 76)
a) - Schéma pour la veste (figure 76)
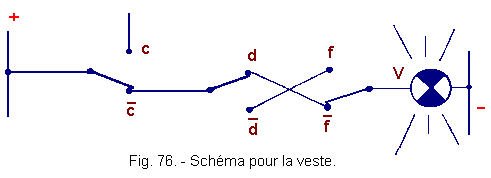
Dans le schéma de la figure 76, on
a représenté le cas ![]() ,
c'est-à-dire que la lampe (prendre ta veste) est allumée, puisque le temps est doux.
,
c'est-à-dire que la lampe (prendre ta veste) est allumée, puisque le temps est doux.
Il est facile de comprendre que la
lampe (prendre ta veste) sera également allumée pour les interrupteurs
position ![]() ,
c'est-à-dire temps doux.
,
c'est-à-dire temps doux.
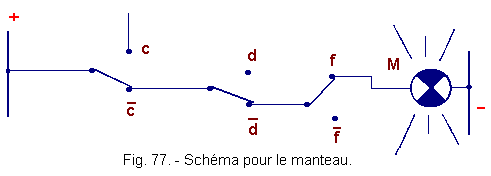
![]() b) - Schéma relatif au manteau (figure 77)
b) - Schéma relatif au manteau (figure 77)
En utilisant les mêmes conventions,
on peut, connaissant l'égalité ![]() ,
établir le schéma.
,
établir le schéma.
![]() c) - Schéma relatif à l'imperméable (figure 78) :
c) - Schéma relatif à l'imperméable (figure 78) :
![]()
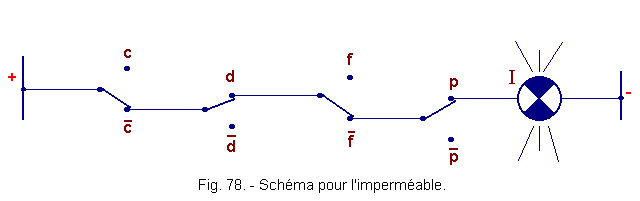
![]() d) - Schéma relatif au parapluie (figure 79)
d) - Schéma relatif au parapluie (figure 79)
![]()
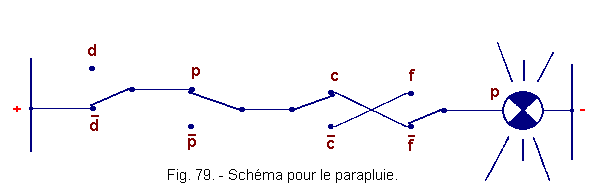
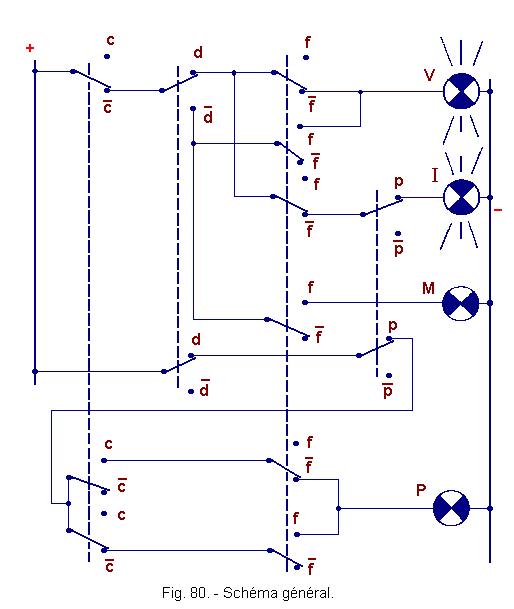
![]() e) - Schéma général (figure 80)
e) - Schéma général (figure 80)
Il représente le cas où les lampes V et I sont allumées.
Dans la table de vérité (figure 70), nous avons prévu une colonne dénommée "impossibilités" ou pannes du système.
Il y a, en effet, impossibilité absolue à ce que les indications chaud et froid, doux et froid, chaud et doux, etc... soient présentes simultanément.
Ces cas sont impossibles ou alors le système est en panne.
On peut, à partir de ces cas, allumer une lampe qui indiquera que le système ne fonctionne pas correctement.
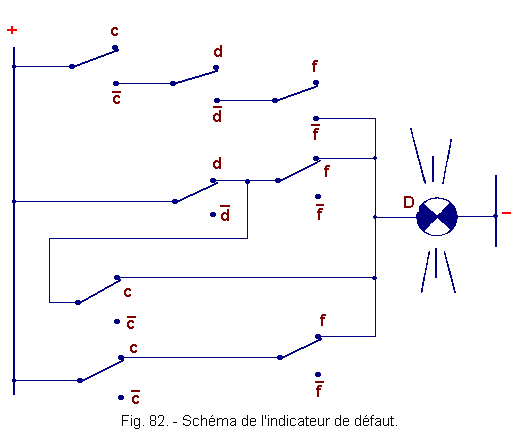
![]() f) - Tableau de Karnaugh détection défaut (figure 81)
f) - Tableau de Karnaugh détection défaut (figure 81)
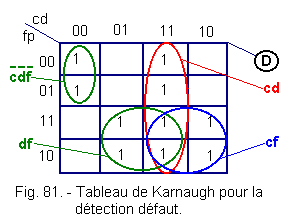
A partir du tableau de Karnaugh, établissons l'équation de D.
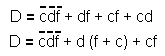
Ceci nous conduit au schéma de l'indicateur défaut représenté figure 82.
![]() 4. 7. - RÉALISATION DU SCHÉMA DE LA SIGNALISATION AU MOYEN DE
SYMBOLES ÉLECTRONIQUES
4. 7. - RÉALISATION DU SCHÉMA DE LA SIGNALISATION AU MOYEN DE
SYMBOLES ÉLECTRONIQUES
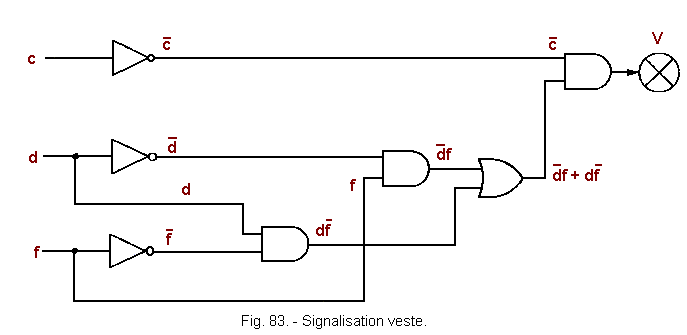
![]() a) - Schéma de la signalisation de la veste (figure 83)
a) - Schéma de la signalisation de la veste (figure 83)
![]()
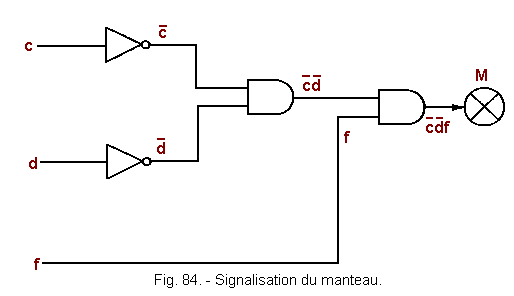
![]() b) - Schéma de la signalisation du manteau (figure 84)
b) - Schéma de la signalisation du manteau (figure 84)
![]()
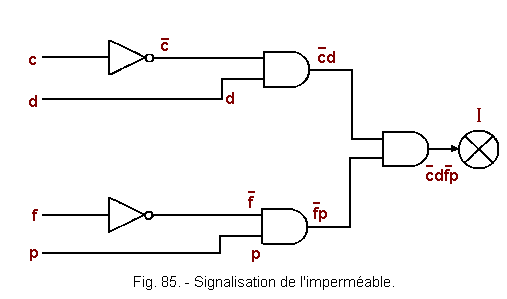
![]() c) - Schéma de la signalisation de l'imperméable (figure 85)
c) - Schéma de la signalisation de l'imperméable (figure 85)
![]()
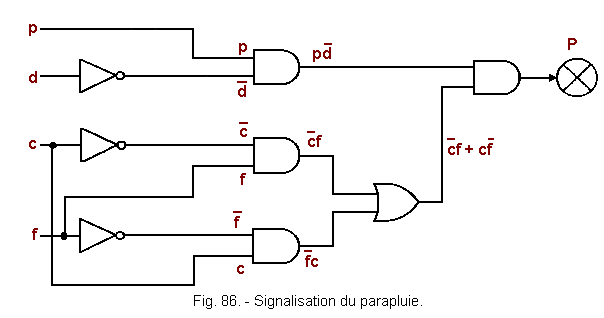
![]() d) - Schéma de la signalisation du parapluie (figure 86)
d) - Schéma de la signalisation du parapluie (figure 86)
![]()
![]() e) - Schéma général (figure 87)
e) - Schéma général (figure 87)
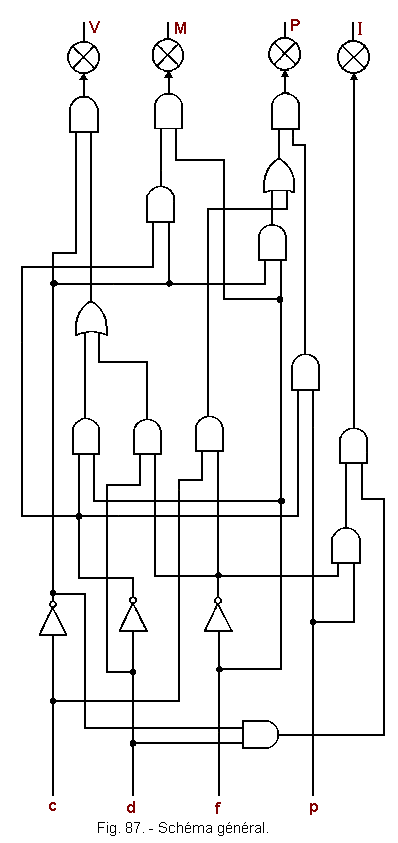
Le schéma général sera constitué par l'assemblage des autres schémas de telle sorte que le nombre d'opérateurs logiques soit minimum.
A cet effet, on examine les schémas
partiels et sachant par exemple que ![]() est utilisé dans les schémas partiels de V
et de P on peut ainsi n'utiliser qu'un seul
inverseur pour produire le signal
est utilisé dans les schémas partiels de V
et de P on peut ainsi n'utiliser qu'un seul
inverseur pour produire le signal ![]() à partir de la variable d. On réussit
ainsi avec un peu de bon sens à rassembler l'ensemble en un seul schéma.
à partir de la variable d. On réussit
ainsi avec un peu de bon sens à rassembler l'ensemble en un seul schéma.
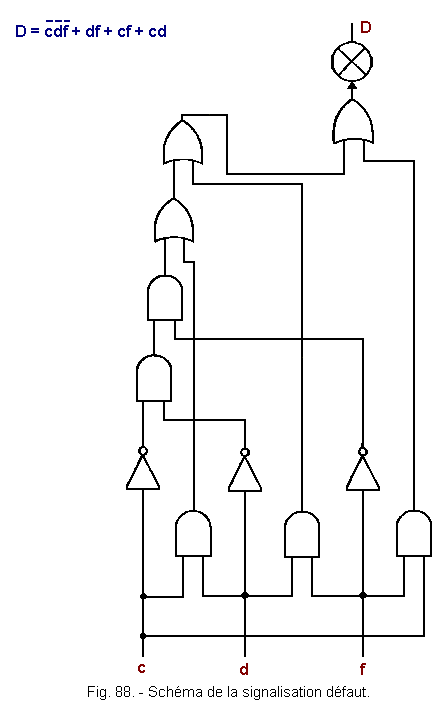
![]() f) - Schéma de la signalisation défaut (figure 88)
f) - Schéma de la signalisation défaut (figure 88)
Dans la prochaine théorie, nous examinerons d'une part de nouvelles méthodes pour transformer les expressions Booléennes et d'autre part des circuits logiques dérivés des trois circuits fondamentaux ET, OU, NON, vus dans cette théorie.
Les circuits examinés jusqu'à présent sont la base de tous les montages dits "combinatoires" c'est-à-dire dont l'état (1 ou 0) des sorties ne dépend que de l'état des entrées au moment où nous examinons le montage.
Nous terminons ainsi cette 2ème leçon.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente |
 Page suivante Page suivante |
Nombre de pages vues, à partir de cette date : le 15 JUILLET 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.