Formulaire 1. 3. - Électrotechnique :
NOTA :
Comme dans les formulaires précédents, les unités utilisées dans les calculs sont empruntées au système S.I.. Les formules contenues dans ce rappel concernent l'électrotechnique et les condensateurs.
![]() FORMULE 99 -
Calcul de la puissance électrique d'un appareil relié au secteur connaissant
le temps de fonctionnement, le nombre correspondant de tours du disque visible au compteur et le nombre de tours par kilowatt-heure indiqué pour chaque type
de compteur.
FORMULE 99 -
Calcul de la puissance électrique d'un appareil relié au secteur connaissant
le temps de fonctionnement, le nombre correspondant de tours du disque visible au compteur et le nombre de tours par kilowatt-heure indiqué pour chaque type
de compteur.
Calculer la puissance électrique d'un appareil relié au secteur
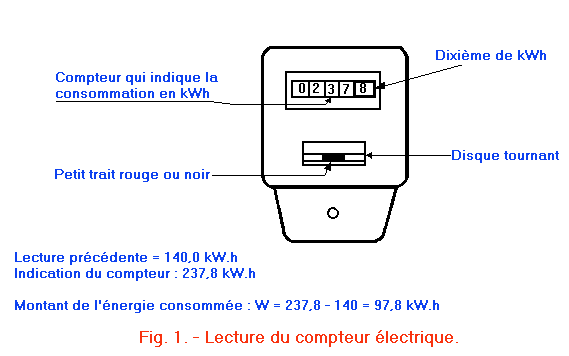
Énoncé : La puissance électrique, exprimée en watts, s'obtient en multipliant par 3 600 000 le nombre de tours du disque tournant (figure 1) et en divisant le produit obtenu par le nombre de tours par kilowatt-heure (2 160 tours / kW.h dans le cas du compteur de la figure 1) et par le temps de fonctionnement exprimé en secondes.
P = (3 600 000 x n) / (N x t)
P = puissance électrique en W (watt)
n = nombre de tours du disque du compteur
N = nombre de tours par kilowatt-heure (tours / kW.h) du compteur
t = temps en secondes mis par le disque pour accomplir 'n' tours
Exemple :
Données : n = 18 tours (comptés lorsque l'appareil dont on veut déterminer la puissance électrique est branché au secteur) ; N = 2 160 / kW.h (indiqués sur le cadran du compteur de la figure 1) ; t = 30 s (temps mis pour accomplir 18 tours, mesuré avec un chronomètre).
Puissance électrique de l'appareil :
P = (3 600 000 x 18) / (2 160 x 30) = 64 800 000 / 64 800 = 1 000 W
OBSERVATION :
Pour établir le nombre de tours (n) accomplis par le disque tournant du compteur, on compte combien de fois, pendant le temps considéré, le petit trait rouge ou noir (figure 1) passe devant la petite fenêtre à travers laquelle on voit ce disque
Sur les compteurs, l'indication du nombre de "tours au kilowatt-heure" est presque toujours remplacée par l'indication équivalente "tour par kilowatt-heure" ou bien par le symbole tours / kW.h.
![]() FORMULE 100 - Calcul
du coût de l'énergie électrique consommée par un appareil connaissant la quantité d'énergie consommée et le prix unitaire, exprimé en francs par
kilowatt-heure.
FORMULE 100 - Calcul
du coût de l'énergie électrique consommée par un appareil connaissant la quantité d'énergie consommée et le prix unitaire, exprimé en francs par
kilowatt-heure.
Calculer le coût de l'énergie électrique consommée par un appareil
C = pW
C = coût de l'énergie électrique en F (franc) "mais maintenant c'est en euro" !
p = prix unitaire de l'énergie électrique en F / kW.h (franc par kilowatt-heure)
W = énergie électrique en kW.h (kilowatt-heure)
-
Exemple :
Données : p = 0,40 F kW.h ; W = 97,8 kW.h (voir les indications portées à la figure 1).
Coût : C = 0,40 x 97,8 = 39,12 F
![]() FORMULE 101 -
Calcul du coût à l'heure de l'énergie
consommée par un appareil électrique connaissant la puissance de l'appareil et le prix unitaire de l'énergie.
FORMULE 101 -
Calcul du coût à l'heure de l'énergie
consommée par un appareil électrique connaissant la puissance de l'appareil et le prix unitaire de l'énergie.
Calculer le coût à l'heure de l'énergie consommée par un appareil électrique
Énoncé : Le coût à l'heure, exprimé en francs, de l'énergie consommée par un appareil électrique s'obtient en divisant par 1 000 le produit entre la puissance, exprimée en watts, et le prix unitaire, exprimé en francs par kilowatt-heure.
C / h = P p / 1 000
C / h = coût à l'heure en F (franc)
P = puissance électrique en W (watt)
p = prix unitaire de l'énergie électrique en F / kW.h (franc par kilowatt-heure)
-
Exemple :
Données : P = 100 W (puissance d'une petite lampe) ; p = 0,40 F / kW.h
Coût à l'heure : C / h = (100 x 0,40) / 1 000 = 0,04 F soit 4 centimes
![]() FORMULE 102 -
Calcul de la capacité d'un corps, connaissant la quantité d'électricité et le potentiel de ce corps.
FORMULE 102 -
Calcul de la capacité d'un corps, connaissant la quantité d'électricité et le potentiel de ce corps.
Calculer la capacité d'un corps
Énoncé : La capacité électrique, exprimée en farads, s'obtient en divisant la quantité d'électricité, exprimée en coulombs, par le potentiel exprimé en volts.
C = Q / V
C = capacité électrique en F (farad)
Q = quantité d'électricité en C (coulomb)
V = potentiel (volt)
-
Exemple :
Données : Q = 0,00002 C ; V = 10 V
Capacité électrique : C = 0,00002 / 10 = 0,000002 = 2 x 10-6 F
OBSERVATION :
Puisque la capacité électrique calculée est relativement petite, on peut exprimer le résultat en microfarads (µF), 1 µF = 10-6 F.
D'où C = 2 µF
![]() FORMULE 103 - Calcul
de la capacité d'un condensateur, connaissant la quantité d'électricité présente
sur une des armatures et la différence de potentiel entre les armatures.
FORMULE 103 - Calcul
de la capacité d'un condensateur, connaissant la quantité d'électricité présente
sur une des armatures et la différence de potentiel entre les armatures.
Calculer la capacité d'un condensateur
Énoncé : La capacité d'un condensateur, exprimée en farads s'obtient en divisant la quantité d'électricité exprimée en coulombs, présente sur l'une ou l'autre armature, par la différence de potentiel entre ces armatures, exprimée en volts.
C = Q / V
C = capacité du condensateur en F (farad)
Q = quantité d'électricité en C (coulomb)
V = différence de potentiel en V (volt)
La présente formule est semblable à la formule 102 et les grandeurs qu'elle contient sont exprimées dans les mêmes unités de mesure ; c'est pourquoi les procédés de calcul sont identiques dans les deux cas.
-
Exemple :
Données : Q = 0,000008 C ; V = 200 V
Capacité du condensateur : C = 0,000008 / 200 = 4 x 10-8 F
OBSERVATION :
D'une façon générale, les capacités des condensateurs sont très petites par rapport à l'unité de mesure, qui est le farad, et pour cette raison, on utilise couramment les sous-multiples du farad, soit le microfarad (µF ; 1 µF = 10-6 F), soit le nanofarad (nF ; 1 nF = 10-9 F) et le picofarad (pF ; 1 pF = 10-12). En exprimant le résultat de l'exemple précédent, en utilisant les divers sous-multiples du farad, on obtient :
C = 4 x 10-8 F = 0,04 µF = 40 nF = 40 000 pF
![]() FORMULE 104 -
Calcul de la quantité d'électricité présente sur l'une ou l'autre armature d'un condensateur, connaissant la différence de potentiel entre les armatures
et la capacité du condensateur.
FORMULE 104 -
Calcul de la quantité d'électricité présente sur l'une ou l'autre armature d'un condensateur, connaissant la différence de potentiel entre les armatures
et la capacité du condensateur.
Calculer la quantité d'électricité présente sur l'une ou l'autre armature d'un condensateur
Q = CV
Q = quantité d'électricité en C (coulomb)
C = capacité en F (farad)
V = différence de potentiel en V (volt)
(Cette formule est tirée de la formule 103).
-
Exemple :
Données : C = 20 nF = 2 x 10-8 F (pour l'équivalence entre le nanofarad et l'unité farad, voir l'observation qui suit la formule 103) ; V = 500 V.
Quantité d'électricité présente sur une armature du condensateur :
Q = 2 x 10-8 x 500 = 10-5 C
![]() FORMULE 105 -
Calcul de la différence de potentiel (tension) existant entre les
armatures d'un condensateur, connaissant la quantité d'électricité présente sur une armature et la capacité du condensateur.
FORMULE 105 -
Calcul de la différence de potentiel (tension) existant entre les
armatures d'un condensateur, connaissant la quantité d'électricité présente sur une armature et la capacité du condensateur.
Calculer la différence de potentiel existant entre les armatures d'un condensateur
V = Q / C
V = différence de potentiel en V (volt)
Q = quantité d'électricité en C (coulomb)
C = capacité en F (farad)
(Cette formule est tirée de la formule 103).
-
Exemple :
Données : Q = 0,0006 C ; C = 5 µF = 5 x 10-6 F (pour l'équivalence entre le microfarad et l'unité de mesure farad, voir l'observation qui suit la formule 103).
Différence de potentiel existant entre les armatures du condensateur :
V = 0,0006 / (5 x 10-6) = 120 V
![]() FORMULE 106 -
Calcul de la constante diélectrique absolue d'un matériau, connaissant la constante diélectrique absolue du vide (ou de l'air) et la constante diélectrique
relative au vide (ou à l'air) de ce même matériau.
FORMULE 106 -
Calcul de la constante diélectrique absolue d'un matériau, connaissant la constante diélectrique absolue du vide (ou de l'air) et la constante diélectrique
relative au vide (ou à l'air) de ce même matériau.
Calculer la constante diélectrique absolue d'un matériau
Énoncé : La constante diélectrique absolue d'un matériau, exprimée en picofarad par mètre, s'obtient en multipliant la constante diélectrique relative au vide (ou à l'air) du matériau par la constante diélectrique absolue du vide (ou de l'air), exprimée en picofarad par mètre.
e = eo x er
e = constante diélectrique absolue d'un matériau en pF / m (picofarad par mètre).
eo = constante diélectrique absolue du vide (8,86 pF / m (picofarad par mètre).
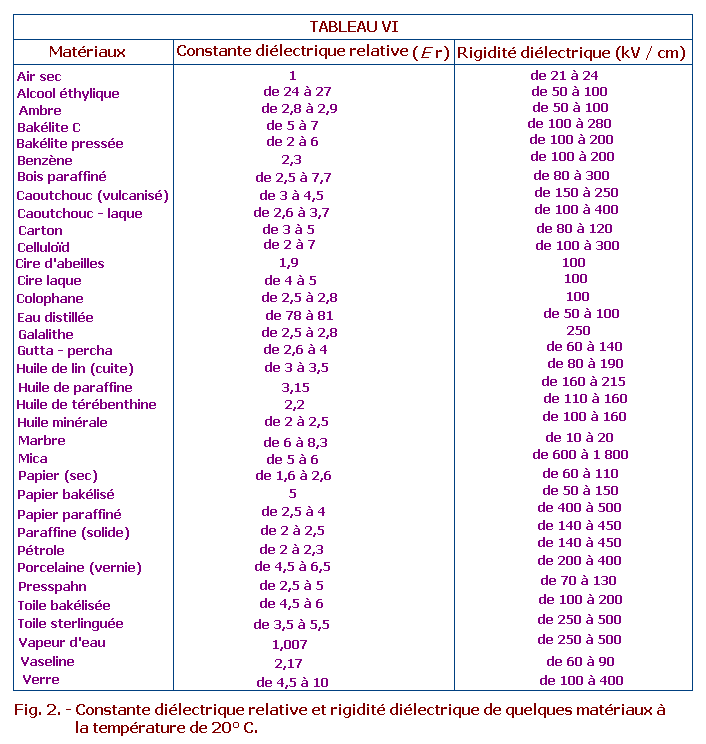
er = constante diélectrique relative du matériau (voir tableau VI, figure 2).
-
Exemple :
Données : eo = 8,86 pF / m ; er = 5 (constante diélectrique relative au carton bakélisé, voir tableau VI, figure 2).
Constante diélectrique absolue du carton bakélisé :
e = 8,86 x 5 = 44,3 pF / m
OBSERVATION :
Parfois, dans les livres de physique et dans les manuels techniques, cette même constante diélectrique absolue est exprimée en farad par mètre (F / m). Le farad par mètre est l'unité de mesure adoptée dans le système international, le picofarad par centimètre et le picofarad par mètre sont des sous-multiples de la même unité :
1 pF / cm = 10-10 F / m ; 1 F / m = 1010 pF / cm
1 pF / m = 10-12 F / m ; 1 F / m = 1012 pF / m
1 pF / cm = 100 pF / m ; 1 pF / m = 0,01 pF / cm
Sur le tableau VI figure 2, on a indiqué les constantes diélectriques relatives au vide, ou à l'air sec, de quelques matériaux isolants qui peuvent présenter un intérêt pour l'électronicien.
![]() FORMULE 107 -
Calcul de la constante diélectrique relative
d'un matériau, connaissant les constantes diélectriques absolues du vide (ou de l'air) et du matériau.
FORMULE 107 -
Calcul de la constante diélectrique relative
d'un matériau, connaissant les constantes diélectriques absolues du vide (ou de l'air) et du matériau.
Calculer la constante diélectrique relative d'un matériau
er = e / eo
er = constante diélectrique relative du matériau
e = constante diélectrique absolue du matériau en pF / m (picofarad par mètre)
eo = constante diélectrique absolue du vide 8,86 pF / m (picofarad / m)
(Cette formule est tirée de la formule 106).
-
Exemple :
Données : e = 16,834 pF / m (constante diélectrique absolue de la cire d'abeilles).
eo = 8,86 pF / m (constante diélectrique absolue du vide ; voir l'observation qui suit la formule 106.
Constante diélectrique relative à la cire d'abeilles : er = 16,834 / 8,86 = 1,9
(Valeur indiquée au tableau VI, figure 2).
![]() FORMULE 108 -
Calcul de la capacité d'un condensateur à
air, formé par deux plaques égales, planes et parallèles, connaissant leur
surface, la distance entre les superficies en présence et la constante diélectrique absolue de l'air.
FORMULE 108 -
Calcul de la capacité d'un condensateur à
air, formé par deux plaques égales, planes et parallèles, connaissant leur
surface, la distance entre les superficies en présence et la constante diélectrique absolue de l'air.
Calculer la capacité d'un condensateur à air
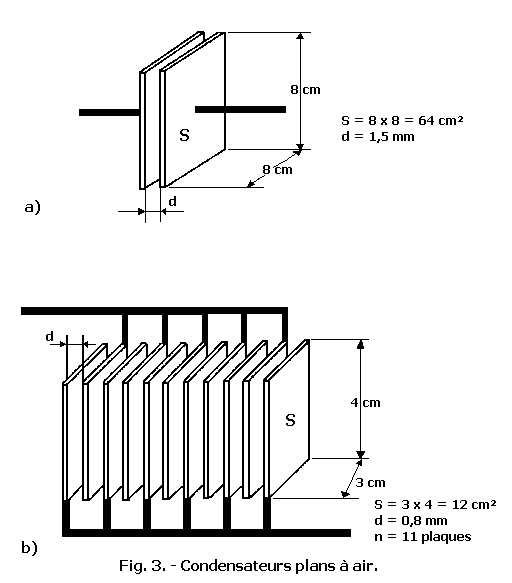
Énoncé : La capacité du condensateur à air (figure 3-a), exprimée en picofarad, s'obtient en multipliant la constante diélectrique absolue de l'air (8,86 pF / m ; formule 106) par la surface d'une plaque, exprimée en centimètres carrès et en divisant le produit obtenu par la distance entre les plaques, exprimée en millimètres et multipliée par 10.
C = (eo x S) / (10 x d)
C = capacité du condensateur en pF (picofarad)
eo = constante diélectrique absolue de l'air = 8,86 pF / m (picofarad par mètre)
S = surface d'une plaque en cm2
d = distance entre les plaques en mm.
-
Exemple : (figure 3-a)
Données : eo 8,86 pF / m ; S = 64 cm2 ; d = 1,5 mm
Capacité du condensateur : C = (8,86 x 64) / (10 x 1,5) = 567,04 / 15 = 37,8 pF
![]() FORMULE 109 -
Calcul de la capacité d'un condensateur à
air formé par trois ou plusieurs plaques égales, planes et parallèles, reliées comme montré figure 3-b, connaissant la surface des plaques, la distance qui
les sépare, le nombre de plaques et la constante diélectrique absolue de l'air.
FORMULE 109 -
Calcul de la capacité d'un condensateur à
air formé par trois ou plusieurs plaques égales, planes et parallèles, reliées comme montré figure 3-b, connaissant la surface des plaques, la distance qui
les sépare, le nombre de plaques et la constante diélectrique absolue de l'air.
Calculer la capacité d'un condensateur à air formé par trois ou plusieurs plaques égales
Énoncé : La capacité d'un condensateur à air (figure 3-b) s'obtient en multipliant la capacité de deux plaques adjacentes, calculée avec la formule 108, par le nombre de plaques moins une.
C = (Eo x S) / (10 x d) x (n - 1)
C = capacité du condensateur en pF (picofarad)
Eo
= constante diélectrique absolue de l'air =
8,86 pF / m (picofarad par mètre)
S = surface d'une plaque en cm2
d = distance entre les plaques en mm
n = nombre de plaques
-
Exemple :
Données :
Eo = 8,86 pF / m ; S = 12 cm2 ; d = 0,8 mm
; n = 11 plaques
Capacité du condensateur :
C = (8,86 x 12) / (10 x 0,8) x (11 - 1) = (106,32 / 8) x 10 = 13,29 x 10 = 132,9 pF
![]() FORMULE 110 - Calcul
de l'énergie électrique emmagasinée par un condensateur, connaissant la quantité d'électricité présente sur l'une ou l'autre armature et la tension
existante entre elles.
FORMULE 110 - Calcul
de l'énergie électrique emmagasinée par un condensateur, connaissant la quantité d'électricité présente sur l'une ou l'autre armature et la tension
existante entre elles.
Calculer l'énergie électrique emmagasinée par un condensateur
Énoncé : L'énergie emmagasinée par un condensateur, exprimée en joules, s'obtient en multipliant la quantité d'électricité présente sur une armature, exprimée en coulombs, par la tension entre les armatures, exprimée en volts et en divisant par 2 le produit obtenue.
W = QV / 2
W = énergie électrique en J (joule)
Q = quantité d'électricité en C (coulomb)
V = tension en V (volt)
-
Exemple :
Données : Q = 0,0004 C (quantité d'électricité présente sur une armature du condensateur) ;
V = 200 V (tension entre les armatures du condensateur).
Énergie électrique emmagasinée par le condensateur :
W = (0,0004 x 200) / 2 = 0,08 / 2 = 0,04 J
![]() FORMULE 111 -
Calcul de la quantité d'électricité présente
sur l'armature d'un condensateur, connaissant la valeur de l'énergie emmagasinée par le condensateur et la tension existant entre ses armatures.
FORMULE 111 -
Calcul de la quantité d'électricité présente
sur l'armature d'un condensateur, connaissant la valeur de l'énergie emmagasinée par le condensateur et la tension existant entre ses armatures.
Calculer la quantité d'électricité présente sur l'armature d'un condensateur
Q = 2W / V
Q = quantité d'électricité en C (coulomb)
W = énergie électrique en J (joule)
V = tension en V (volt)
(Cette formule est tirée de la formule 110)
-
Exemple :
Données : W = 0,08 J = 0,08 J (énergie emmagasinée par le condensateur).
V = 160 V (tension entre les armatures du condensateur).
Quantité d'électricité présente sur une armature du condensateur :
Q = (2 x 0,08) / 160 = 0,16 / 160 = 0,001 C
![]() FORMULE 112 - Calcul
de la tension existante entre les armatures d'un condensateur, connaissant la
valeur de l'énergie emmagasinée et la quantité d'électricité présente sur une armature.
FORMULE 112 - Calcul
de la tension existante entre les armatures d'un condensateur, connaissant la
valeur de l'énergie emmagasinée et la quantité d'électricité présente sur une armature.
Calculer la tension existante entre les armatures d'un condensateur
V = 2W / Q
V = tension en V (volt)
W = énergie électrique en J (joule)
Q = quantité d'électricité en C (coulomb)
(Cette formule est tirée de la formule 110)
-
Exemple :
Données : W = 1,5 J (énergie emmagasinée par le condensateur).
Q = 0,06 C (quantité d'électricité présente sur une armature du condensateur).
Tension entre les armatures du condensateur :
V = (2 x 1,5) / 0,06 = 3 / 0,06 = 50 V
![]() FORMULE 113 -
Calcul de l'énergie électrique emmagasinée par un condensateur, connaissant la capacité et la tension existant entre les armatures.
FORMULE 113 -
Calcul de l'énergie électrique emmagasinée par un condensateur, connaissant la capacité et la tension existant entre les armatures.
Calculer l'énergie électrique emmagasinée par un condensateur
Énoncé : L'énergie emmagasinée par un condensateur, exprimée en joules, s'obtient en multipliant la capacité exprimée en farads par le carré de la tension, exprimée en volt et en divisant par deux le produit obtenu.
W = CV2 / 2
W = énergie électrique en J (joule)
C = capacité en F (farad)
V = tension en V (volt)
-
Exemple :
Données : C = 400 µF = 0,0004 F ; V = 50 V
Énergie électrique emmagasinée :
W = (0,0004 x 502) / 2 = (0,0004 x 2 500) / 2 = 1 / 2 = 0,5 J
![]() FORMULE 114 - Calcul de la capacité d'un
condensateur, connaissant la valeur de l'énergie emmagasinée et la tension existant entre les armatures.
FORMULE 114 - Calcul de la capacité d'un
condensateur, connaissant la valeur de l'énergie emmagasinée et la tension existant entre les armatures.
Calculer la capacité d'un condensateur
C = 2W / V2
C = capacité en F (farad)
W = énergie électrique en J (joule)
V = tension en V (volt)
(Cette formule est tirée de la formule 113).
-
Exemple :
Données : W = 0,05 J (énergie emmagasinée par le condensateur).
V = 500 V (tension entre les armatures du condensateurs).
Capacité : C = (2 x 0,05) / 5002 = 0,1 / 250 000 = 4 x 10-7 F = 0,4 µF (microfarad)
![]() FORMULE 115 - Calcul
de la tension existante entre les armatures d'un condensateur, connaissant la valeur de l'énergie emmagasinée et la capacité du condensateur.
FORMULE 115 - Calcul
de la tension existante entre les armatures d'un condensateur, connaissant la valeur de l'énergie emmagasinée et la capacité du condensateur.
Calculer la tension existante entre les armatures d'un condensateur
Énoncé : La tension existant entre les armatures d'un condensateur, exprimée en volts, s'obtient en divisant le double de l'énergie emmagasinée, exprimée en joules, par la capacité exprimée en farads et en extrayant la racine carrée du quotient obtenu.
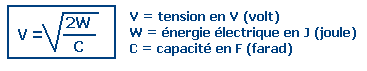
-
Exemple :
Données : W = 4,9 J (énergie électrique emmagasinée par le condensateur).
C = 80 µF = 8 x 10-5 F (capacité du condensateur)
Tension existante entre les armatures du condensateur :
.gif)
![]() FORMULE 116 - Calcul
de l'intensité du champ électrique existant dans le diélectrique d'un condensateur, connaissant la tension et la distance entre les armatures.
FORMULE 116 - Calcul
de l'intensité du champ électrique existant dans le diélectrique d'un condensateur, connaissant la tension et la distance entre les armatures.
Calculer l'intensité du champ électrique existant dans le diélectrique d'un condensateur
Énoncé : L'intensité du champ électrique existant dans le diélectrique d'un condensateur, exprimée en kilovolts par mètre s'obtient en divisant la tension existant entre ses armatures, exprimée en volts, par la distance qui les sépare exprimée en millimètres.
E = V / d
E = intensité du champ électrique en kV / m (kilovolt par mètre)
V = tension en V (volt)
d = distance entre les armatures en mm
-
Exemple :
Données : V = 350 V ; d = 0,7 mm.
Intensité du champ électrique : E = 350 / 0,7 = 500 kV / m
OBSERVATION :
L'intensité maximale du champ électrique admis par un diélectrique est appelée rigidité diélectrique.
Au tableau VI figure 2, à côté des valeurs de la constante diélectrique relative à quelques matériaux isolants (diélectriques), sont portées les valeurs de la rigidité diélectrique. On observera que la rigidité diélectrique, dans ce tableau, est exprimée en kilovolts par centimètre (kV /cm) au lieu de kilovolts par mètre (kV / m), comme indiqué dans la formule 116. Le kilovolt par centimètre et le kilovolt par mètre sont des multiples du volt par mètre (V / m), unité de mesure de l'intensité du champ électrique :
1 kV / m = 1 000 V / m ; 1 kV / cm = 100 000 V / m
1 kV / m = 0,01 kV / cm ; 1 kV / cm = 100 kV / m
![]() FORMULE 117 -
Calcul de l'épaisseur d'une couche isolante,
connaissant la rigidité diélectrique du matériau et la tension électrique qu'il devra soutenir entre l'une et l'autre superficie de l'épaisseur.
FORMULE 117 -
Calcul de l'épaisseur d'une couche isolante,
connaissant la rigidité diélectrique du matériau et la tension électrique qu'il devra soutenir entre l'une et l'autre superficie de l'épaisseur.
Calculer l'épaisseur d'une couche isolante
Énoncé : L'épaisseur de la couche isolante, exprimée en millimètres, s'obtient en divisant la tension, exprimée en volts, par la rigidité diélectrique du matériau, exprimée en kilovolts par centimètre (tableau VI, figure 2) et multipliée par 100.
d = V / (100 x Rd)
d = épaisseur de l'isolant en mm
V = tension en V (volt)
Rd = rigidité diélectrique en kV / cm (kilovolt par centimètre)
-
Exemple :
Données : V = 12 000 Rd (tension à appliquer entre les surfaces opposées du diélectrique).
Rd = 600 kV / cm (rigidité diélectrique minimale du mica ; voir tableau VI, figure 2).
Épaisseur de la couche de mica nécessaire pour obtenir l'isolement à la tension indiquée :
d = 12 000 / (100 x 600) = 12 000 / 60 000 = 0,2 mm
![]() FORMULE 118 -
Calcul de la tension qu'une épaisseur de matériau
isolant pourra supporter, connaissant l'épaisseur et la rigidité diélectrique du matériau.
FORMULE 118 -
Calcul de la tension qu'une épaisseur de matériau
isolant pourra supporter, connaissant l'épaisseur et la rigidité diélectrique du matériau.
Calculer la tension qu'une épaisseur de matériau isolant pourra supporter
V = 100 x Rd x d
V = tension en V (volt)
Rd = rigidité diélectrique en kV / cm (kilovolt par centimètre)
d = épaisseur en mm
(Cette formule est tirée de la formule 117)
-
Exemple :
Données : Rd = 400 kV / cm (rigidité diélectrique minimale du papier paraffiné, voir tableau VI, figure 2) ; d = 0,025 mm (épaisseur d'une feuille de papier paraffiné).
Tension que l'on veut appliquer entre les deux pages d'une feuille de papier paraffiné :
V = 100 x 400 x 0,025 = 1 000 V
![]() FORMULE 119 -
Calcul de la capacité totale de deux ou de plusieurs condensateurs reliés en parallèle, connaissant la capacité de
chaque condensateur.
FORMULE 119 -
Calcul de la capacité totale de deux ou de plusieurs condensateurs reliés en parallèle, connaissant la capacité de
chaque condensateur.
Calculer la capacité totale de deux ou de plusieurs condensateurs reliés en parallèle
Énoncé : La capacité totale de deux ou de plusieurs condensateurs reliés en parallèle s'obtient en additionnant leurs capacités.
Ct = C1 + C2 + C3 + ... + Cn
Ct = capacité totale
C1 = capacité du premier condensateur
C2 = capacité du second condensateur
C3 = capacité du troisième condensateur
Cn = capacité du dernier condensateur
Les valeurs de capacité doivent toutes être exprimées avec la même unité de mesure.
-
Exemples :
a) Données : C1 = 10 pF (picofarad) ; C2 = 18 pF ; C3 = 8 pF ; Cn = 24 pF.
Capacité totale : Ct = 10 + 18 + 8 + 24 = 60 pF
b) Données : C1 = 50 nF (nanofarad) ; C2 = 30 nF ; C3 = 15 nF ; C4 = 60 nF ; Cn = 5 nF.
Capacité totale : Ct = 50 + 30 + 15 + 60 + 5 = 160 nF
c) Données : C1 = 2 µF (microfarad) ; C2 = 5 µF ; C3 = 5 µF
Capacité totale : Ct = 2 + 5 + 5 = 12 µF
![]() FORMULE 120 -
Calcul de la capacité équivalente de deux ou de plusieurs condensateurs de valeur égale, reliés en série, connaissant
leur capacité.
FORMULE 120 -
Calcul de la capacité équivalente de deux ou de plusieurs condensateurs de valeur égale, reliés en série, connaissant
leur capacité.
Calculer la capacité équivalente de deux ou de plusieurs condensateurs de valeur égale
Énoncé : La capacité équivalente de deux ou de plusieurs condensateurs ayant la même capacité, reliés en série, s'obtient en divisant la capacité d'un condensateur par le nombre de condensateurs.
Ceq = C / n
Ceq = capacité équivalente
C = capacité de chaque condensateur
n = nombre de condensateurs.
La capacité équivalente est obtenue avec la même unité de mesure que celle utilisée pour indiquer la capacité des condensateurs.
-
Exemples :
a) Données : C = 420 pF (picofarad) ; n = 2.
Capacité équivalente : Ceq = 420 / 2 = 210 pF.
b) Données : C = 40 nF (nanofarad) ; n = 4
Capacité équivalente : Ceq = 40 / 4 = 10 nF.
c) Données : C = 2 µF (microfarad) ; n = 3
Capacité équivalente : Ceq = 2 / 3
![]() FORMULE 121 -
Calcul de la capacité équivalente de deux condensateurs de valeur différente, reliés en série, connaissant leur
capacité respective.
FORMULE 121 -
Calcul de la capacité équivalente de deux condensateurs de valeur différente, reliés en série, connaissant leur
capacité respective.
Calculer la capacité équivalente de deux condensateurs de valeur différente, reliés en série
Énoncé : La capacité équivalente de deux condensateurs reliés en série s'obtient en multipliant la capacité des deux condensateurs et en divisant le produit obtenu par la somme de ces capacités.
Ceq = (C1 x C2) / (C1 + C2)
Ceq = capacité équivalente
C1 = capacité d'un condensateur
C2 = capacité de l'autre condensateur.
Les valeurs de capacité doivent toutes être exprimées avec la même unité de mesure.
-
Exemple :
Données : C1 = 40 nF (nanofarad) ; C2 = 60 nF.
Capacité équivalente des deux condensateurs reliés en série :
Ceq = (40 x 60) / (40 + 60) = 2 400 / 100 = 24 nF
![]() FORMULE 122 - Calcul
de la capacité d'un condensateur à relier en série à un autre condensateur de capacité connue, pour obtenir une capacité équivalente donnée.
FORMULE 122 - Calcul
de la capacité d'un condensateur à relier en série à un autre condensateur de capacité connue, pour obtenir une capacité équivalente donnée.
Calculer la capacité d'un condensateur à relier en série à un autre condensateur de capacité connue
Énoncé : La capacité d'un condensateur à relier en série à un autre condensateur, pour obtenir une capacité équivalente donnée, se calcule en multipliant la capacité du condensateur connu par la capacité équivalente et en divisant le produit par la différence de ces mêmes valeurs.
Ci = (C x Ceq) / (C - Ceq)
Ci = capacité inconnue
C = capacité du condensateur disponible
Ceq = capacité équivalente que l'on veut obtenir
Les valeurs de capacité doivent toutes être exprimées avec la même unité de mesure.
-
Exemple :
Données : C = 500 pF (picofarad) ; Ceq = 400 pF.
Capacité inconnue : Ci = (500 x 400) / (500 - 400) = 200 000 / 100 = 2 000 pF
![]() FORMULE 123 -
Calcul de la capacité équivalente de plusieurs condensateurs reliés en série, connaissant leur capacité.
FORMULE 123 -
Calcul de la capacité équivalente de plusieurs condensateurs reliés en série, connaissant leur capacité.
Calculer la capacité équivalente de plusieurs condensateurs reliés en série
Énoncé : La capacité équivalente de plusieurs condensateurs reliés en série, s'obtient en exécutant les calculs en trois temps : on calcule d'abord l'inverse de la capacité de chaque condensateur, ce qui revient à diviser le nombre 1 par la valeur de la capacité. Ensuite, on additionne les valeurs des inverses. Enfin, on calcule la capacité équivalente en divisant le nombre 1 par la somme des inverses.
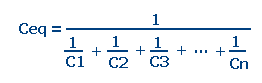
Ceq = capacité équivalente
C1 = capacité du premier condensateur
C2 = capacité du second condensateur
C3 = capacité du troisième condensateur
Cn = capacité du dernier condensateur
Les valeurs de capacité doivent toutes être exprimées avec la même unité de mesure.
-
Exemple :
Données : C1 = 500 pF (picofarad) ; C2 = 2 000 pF ; C3 = 400 pF ; Cn = 200 pF.
Capacité équivalente :
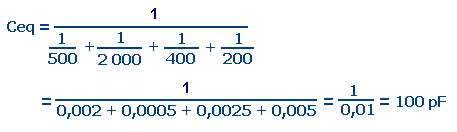
OBSERVATION :
Si l'on
doit calculer la capacité équivalente de deux condensateurs reliés en série,
on peut utiliser la formule 123, mais il est plus simple de recourir à la
formule 121 ; En
outre, dans le cas où les capacités des condensateurs reliés en série sont égales, on peut alors utiliser
la formule 120.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet.
|
|
 Page précédente Page précédente
|
 Page suivante Page suivante |
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.
 Puissance électrique d'un appareil
Puissance électrique d'un appareil