Le diélectriqueCapacité Électrique et Diélectrique d'un Condensateur :
CAPACITÉ ÉLECTRIQUE :
Après avoir étudié les résistances, voyons le fonctionnement des condensateurs.
Puisqu'il faut des quantités d'électricité différentes pour porter des corps de dimensions différentes à un même potentiel électrique, nous pouvons caractériser chaque corps par la quantité d'électricité qu'il doit posséder pour atteindre le potentiel de un volt ; cette quantité d'électricité est la capacité électrique (symbole C) du corps.
Pour un corps qui possède une quantité d'électricité déterminée, et qui se trouve à un potentiel déterminé, on obtient la capacité électrique en divisant la quantité d'électricité par le potentiel.
C = Q / V
Par exemple, on obtient la capacité d'un corps qui a une quantité d'électricité de quatre coulombs et qui se trouve à un potentiel de huit volts en faisant la division 4 / 8 = 0,5 ; il faut donc 0,5 coulomb pour atteindre le potentiel de un volt, c'est-à-dire que la capacité électrique est de 0,5 coulomb par volt.
Ainsi, la capacité électrique se mesure en coulomb par volt, unité de mesure à laquelle fut donné le nom de farad (symbole F), en l'honneur du savant Michaël FARADAY, déjà cité pour ses recherches sur les solutions électrolytiques. Le corps considéré dans notre exemple a donc une capacité de 0,5 farad.
Il faut noter qu'une sphère de la dimension de la terre aurait une capacité d'environ 1 F ; le farad est donc une unité de mesure beaucoup trop grande.
Pour cette raison, en pratique, nous utilisons principalement les sous-multiples du farad soit :
Le microfarad (symbole µF) qui équivaut à un millionième de farad (10-6 F).
Le nanofarad (symbole nF) qui équivaut à un milliardième de farad (10-9 F soit 10-3 µF).
Le picofarad (symbole pF) qui équivaut à un millionième de millionième de farad (10-12 F, soit 10-6 µF ou 10-3 nF).
LE CONDENSATEUR
La capacité d'un corps dépend en premier lieu de la présence dans son voisinage d'autres corps électrisés.
Cette constatation peut être faite expérimentalement, en considérant les deux plaques métalliques de la figure 1.
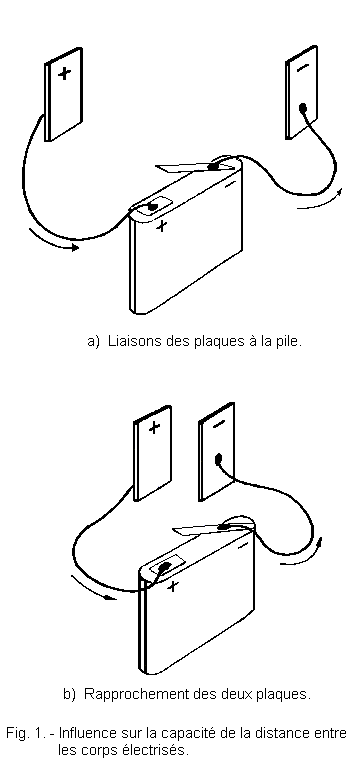
Ces deux plaques métalliques rigoureusement identiques sont reliées chacune à un pôle d'une pile, et se chargent d'électricité positive ou négative suivant le pôle auquel elles sont reliées.
A la figure 1-a, nous constatons que le processus de charge des deux plaques est très simple, un certain nombre d'électrons va du pôle négatif de la pile à la plaque qui lui est reliée, la chargeant négativement, tandis que le pôle positif de la pile attire un nombre égal d'électrons à la plaque qui lui est reliée ; celle-ci se charge positivement.
Dans les conducteurs qui relient chaque plaque à la pile, il se crée un mouvement d'électrons dont le sens est indiqué figure 1-a. Le mouvement d'électrons cesse de lui-même lorsque la quantité d'électrons présente sur chaque plaque est telle que chaque plaque est au même potentiel que le pôle de la pile qui lui est relié.
Entre les deux plaques existe la même différence de potentiel qu'aux bornes de la pile.
Comme nous l'avons vu précédemment, la quantité d'électricité que pourra emmagasiner chaque plaque dépend de sa capacité, or, les deux plaques étant identiques, elles possèdent la même capacité donc elles emmagasinent deux quantités d'électricité égales mais l'une est positive et l'autre négative.
Supposons à présent que nous rapprochons les deux plaques, en les disposant bien en face l'une de l'autre, comme indiqué sur la figure 1-b, mais en évitant tout contact entre elles pour ne pas mettre la pile en court-circuit.
De ce rapprochement des plaques, il apparaît une nouvelle circulation d'électrons, dans le sens indiqué figure 1-b et donc une augmentation de la quantité d'électricité contenue sur chaque plaque.
Pour le moment, limitons-nous à constater cet état de fait, l'explication en sera donnée plus tard.
Nous constatons que la quantité d'électricité sur chaque plaque a augmenté, bien que le potentiel de celles-ci n'ait pas changé.
Nous pouvons donc affirmer qu'en rapprochant deux plaques, leur capacité augmente.
Puisque la capacité change en faisant varier la distance entre les plaques, nous ne devons plus tenir compte d'une seule plaque mais considérer un ensemble constitué de deux plaques placées face à face à une distance déterminée, de la manière indiquée figure 2.
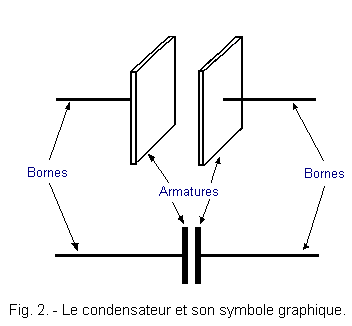
Cette disposition représente le type de condensateur le plus simple, qui est justement constitué de deux plaques en regard, appelées pour la circonstance armatures, munies de deux conducteurs (appelés bornes) pour leur raccordement aux circuits. A la figure 2 vous est également donné le symbole graphique du condensateur tel que vous le rencontrez dans les schémas électriques.
Quelles que soient leurs caractéristiques ou le fabricant qui les conçoit, un condensateur est toujours constitué de deux armatures séparées par un isolant.
Pour définir la capacité d'un condensateur, il faut tenir compte de ses deux armatures et considérer ainsi la différence de potentiel existant entre elles.
Bien qu'un condensateur se compose dans tous les cas de deux armatures, une seule quantité d'électricité entre en ligne de compte. Elle est constituée des électrons qui, comme nous l'avons vu dans la figure 1, sont passés de l'armature devenue positive sur l'armature devenue négative et ceci par l'intermédiaire de la pile.
Nous devons seulement considérer la quantité d'électrons manquante sur une armature ou bien celle présente en surplus sur l'autre, puisqu'il s'agit, en tout état de cause, de la même quantité d'électricité qui s'est transférée d'une armature sur l'autre.
La capacité d'un condensateur s'obtient en divisant la quantité d'électricité présente sur l'une de ses armatures par la différence de potentiel existant entre ses armatures.
Le condensateur est un élément des circuits électriques et se caractérise par sa capacité, comme la résistance est caractérisée par sa valeur résistive.
Nous connaissons le rôle de la résistance qui est de produire des chutes de tension, et nous verrons ultérieurement le rôle du condensateur.
LE DIÉLECTRIQUE
Le premier condensateur fut réalisé par le hollandais Pierre MUSSCHENBROCK (1692 - 1761) qui en découvrit les propriétés presque par hasard en même temps que l'allemand Georges VON KLEIST (1700 - 1748), au cours de ses expériences sur l'électricité.
Les expériences de ces savants ont montré l'influence qu'à sur la capacité d'un condensateur la matière isolante placée entre ses armatures, et qui constitue son diélectrique.
Le diélectrique du condensateur de la figure 2 est l'air et pour cette raison, ce condensateur est appelé condensateur à air.
Le diélectrique des condensateurs peut aussi être un autre matériau isolant tel que le mica, la papier paraffiné, le polystyrène, certaines substances céramiques, etc...
Très vite, les savants constatèrent que la capacité d'un condensateur à air augmentait quand ils mettaient entre ses armatures un diélectrique solide ; par exemple, une plaque de mica disposée entre les armatures d'un condensateur fait augmenter sa capacité de cinq à six fois, selon le mica employé.
Ce qui signifie que, en ayant toujours la même différence de potentiel entre les armatures du condensateur, la quantité d'électricité présente sur celles-ci devient cinq à six fois supérieure si l'on remplace l'air par la feuille de mica.
Ce comportement est dû au fait que le diélectrique solide mis entre les armatures du condensateur se polarise, comme nous allons le voir.
Considérons la figure 1-a sur laquelle est illustré un condensateur possédant un diélectrique solide. Le diélectrique occupe entièrement l'espace compris entre les deux armatures. Dans cette figure 1-a, apparaissent également quelques atomes du diélectrique, qui, pour simplifier notre explication sont supposés être constitués de quatre électrons gravitant autour du noyau sur une orbite unique.
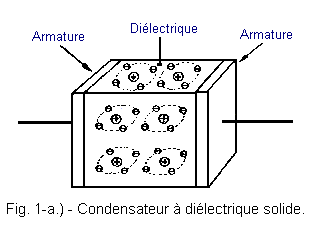
Tant qu'aucune tension n'est appliquée aux bornes du condensateur, les électrons gravitent régulièrement autour de leur noyau respectif (figure 1-a). Si par contre nous relions les armatures du condensateur aux bornes d'une pile comme dans la figure 1-b, les électrons sont attirés par l'armature qui devient positive et repoussée par celle devenant négative.
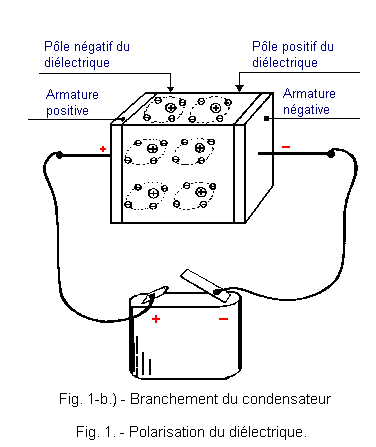
Comme le diélectrique est un isolant, les électrons ne peuvent pas quitter leur orbite, mais par contre, ils la modifient. Les électrons passent plus près de l'armature positive et plus loin de l'armature négative pendant la gravitation autour de leur noyau (figure 1-b).
Si nous considérons le phénomène dans son ensemble, nous voyons qu'il se crée un déplacement d'électrons qui, bien que demeurant liés à leur atome, se rapprochent néanmoins de l'extrémité gauche du diélectrique. Ce déplacement engendre ainsi une dissymétrie dans la distribution des charges électriques à l'intérieur du diélectrique.
L'extrémité gauche du diélectrique vers laquelle se dirigent les électrons devient négative et est appelée pôle négatif, tandis que l'extrémité droite qui voit s'éloigner les électrons est appelée pôle positif.
Nous pouvons dire que le diélectrique se polarise parce que ses extrémités prennent des polarités électriques différentes.
De la polarisation du diélectrique dépend de l'augmentation des charges présentes sur les armatures du condensateur et, en conséquence, cette polarisation détermine une augmentation de sa capacité.
Lorsque nous analyserons l'énergie relative à un condensateur, nous donnerons une explication sur ce fait. Pour le moment, il suffit de se rappeler que la capacité d'un condensateur dépend du matériau isolant dont est constitué son diélectrique, et plus particulièrement de sa polarisation inhérente à tel ou tel type de diélectrique.
CONSTANTE DIÉLECTRIQUE
Deux Condensateurs, dont les armatures sont de même surface et séparées par la même distance mais dont le diélectrique est différent, présentent des capacités différentes.
La différence entre les propriétés des matériaux constituant les diélectriques est caractérisée par la constante diélectrique absolue du matériau.
Le symbole de la constante diélectrique absolue d'un matériau est e (lettre grecque et se lit epsilon) ; son unité est le farad par mètre (symbole F / m).
Tout diélectrique possède sa propre constante diélectrique. Celle de l'air, qui est d'ailleurs considérée comme identique à celle du vide, est appelée constante diélectrique de l'air ou du vide et a pour symbole e0 (epsilon zéro). e0 vaut 1 / 36 P x 109 F / m soit pour faciliter les calculs : 8,85 pF / m.
La connaissance de e0 est très importante car en pratique, il n'est pas coutume d'indiquer la constante diélectrique absolue (e) d'un matériau et vous trouverez plutôt la constante diélectrique relative (er) qui indique le rapport de la constante diélectrique absolue du matériau considéré et de la constante diélectrique de l'air ou du vide.
er = e / e0
La constante diélectrique relative er ne possède pas, quant à elle, d'unité (e0 et e possédant la même unité qu'est le F / m).
A titre indicatif, sont reportées les valeurs de la constante diélectrique relative er de quelques matériaux utilisés pour la réalisation du diélectrique des condensateurs :
|
Matériau |
Constante diélectrique relative er |
|
Air sec |
1 |
|
Papier spécial pour condensateur (KRAFT) |
4,5 |
|
Mica |
5 à 6 |
|
Titanate de Magnésie |
5,4 à 20 |
|
Rutile, Rutiles-zircones, Titanate de calcium |
30 à 220 |
|
Titanates et Zirconates de Baryum |
500 à 15 000 |
|
Polystyrène (Styroflex) |
2,3 |
|
Polytétrafluorétylène (PTFE, Teflon) |
2 |
|
Polymonochlorotrifluorétylène (PCFTE) |
2,3 à 2,8 |
|
Polytéréphtalate d'éthylène (Polyester, Mylar) |
3,1 |
|
Electrolytique à l'aluminium |
9 |
|
Electrolytique au tantale |
11 |
NOTE : La constante diélectrique relative est &galement appel&e permittivité relative, de même que la constante diélectrique absolue est également appelée permittivité absolue.
CALCUL DE LA CAPACITÉ D'UN CONDENSATEUR
Nous savons donc que la capacité d'un condensateur dépend de ses dimensions (surface des armatures et distance entre elles) et de son diélectrique : nous devons donc pouvoir calculer cette capacité d'après ces éléments, de même que nous avons pu déterminer la résistance d'un conducteur d'après ses dimensions et d'après la matière qui le constitue.
Nous avons vu que lorsque nous augmentons la surface des armatures d'un condensateur, nous augmentons la quantité d'électricité présente sur celles-ci et donc aussi la capacité du condensateur : la capacité d'un condensateur est proportionnelle à la surface de ses armatures donc :
C = f (S)
Nous avons vu ensuite que la quantité d'électricité sur les armatures augmente si nous diminuons la distance qui les sépare. Nous pouvons conclure que la capacité d'un condensateur est inversement proportionnelle à la distance qui sépare ses armatures :
C = f (1 / d)
Enfin intervient la constante diélectrique absolue du matériau utilisé. Plus cette constante est élevée, plus grande est la capacité du condensateur :
C = f (e)
De la combinaison des trois relations que nous venons d'établir, la formule générale de calcul d'un condensateur devient donc :
C = e . (S / d)
C : Capacité en F
e : Constante diélectrique absolue en F / m
S : Surface des armatures en m²
d : Distance entre les armatures (ou épaisseur du diélectrique) en m
Toutefois, comme nous considérons le plus souvent la constante diélectrique relative, la formule précédente devient :
C = er . e0 . (S / d)
Après avoir examiné tous les éléments du condensateur qui influent sur sa capacité, nous allons analyser le comportement du condensateur lorsqu'il est inséré dans un circuit électrique de manière à comprendre les raisons pour lesquelles ce composant est très utilisé en pratique.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
 Haut de page |
|
Page précédente
|
 Page suivante |
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.