Expressions Algébriques - Monônes - Polynômes :
PREMIÈRE PARTIE : ALGÈBRE
Nous abordons maintenant notre troisième leçon de mathématiques. Il est composé de deux parties importantes.
La première est consacrée à l'algèbre. Vous connaîtrez ce qu'est une expression algébrique et apprendrez à effectuer des calculs sur les monômes et les polynômes. Vous verrez ensuite ce qu'est une équation et comment la résoudre.
Dans la seconde partie, il sera question des logarithmes. Vous verrez que par leur intermédiaire les calculs complexes avec les puissances et les extractions de racine se transforment en simples multiplications ou divisions.
D'autre part, comme vous êtes maintenant habitués aux développements mathématiques, nous les emploierons désormais de préférence aux explications littérales toujours plus longues et moins précises.
Enfin, comme nous l'avons déjà dit et répété dans les deux premières leçons, nous vous invitons à refaire les exercices cités en exemples, tant au cours de vos lectures que quelque temps après.
1. - EXPRESSIONS ALGÉBRIQUES
1. 1. DÉFINITION
On appelle expression algébrique, un ensemble de lettres et de nombres reliés entre eux par des signes indiquant les opérations à effectuer.
Exemple :
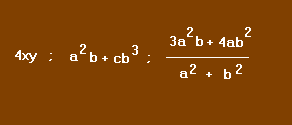
Chaque lettre représente un nombre. Si la même lettre figure plusieurs fois dans la même expression, elle y représente le même nombre. Pour obtenir la valeur numérique de l'expression, il suffit de remplacer chaque lettre par le nombre qu'elle représente.
Exemple : calculez la valeur numérique de :
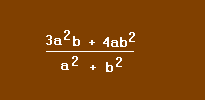
Lorsque a = 1 et b = 2
Nous écrivons :
3 x (1)2 x (2) + 4 x (1) x (2)2 / (1)2 + (2)2 = 6 + 16 / 1 + 4 = 22 / 5 = 4,4
1. 2. - CALCUL DE LA VALEUR NUMÉRIQUE D'UNE EXPRESSION ALGÉBRIQUE
Il faut du soin et de l'attention. Tout ce qui se trouve dans une parenthèse, devra être considéré un nombre unique à prendre comme tel, après l'avoir calculé.
La règle des signes, que nous avons vu, s'applique évidemment dans ces calculs. D'autre part, la règle concernant la suppression des parenthèses précédées du signe + ou - s'applique également :
Exemple : si a = 1 et b = 2, on obtient :
(a + b) X (a - b) = (1 + 2) X (1 - 2) = 3 X (- 1) = - 3
(a + b) X (a + b) = (1 + 2) X (1 + 2) = 3 X 3 = 9
(3a + 2b) - (2a - 3b) = (3 + 4) - (2 - 6) = (7) - (- 4) = 7 + 4 = 11
Les deux premières expressions qui ne diffèrent que par des parenthèses et des signes ont, comme vous le voyez, des valeurs numériques différentes.
1. 3. - DIFFÉRENTES FORMES D'EXPRESSIONS ALGÉBRIQUES
1. 3. 1. - EXPRESSION ALGÉBRIQUE DITE ENTIÈRE
L'expression ne contient pas de lettres au dénominateur.
Exemple :
3a² ; 4ab² + 6b²a² ; 3 / 2 (x² - 2y²)
1. 3. 2. - EXPRESSION ALGÉBRIQUE DITE FRACTIONNAIRE
L'expression contient des lettres au dénominateur.
Exemple :
3a2 / b2 ; 3 / 2 . x2 / (a2 + b2)
1. 3. 3. - Monômes
L'expression ne contient pas de signes d'addition ou de soustraction.
Exemple :
3x2y2 ; 3 / 2 . x2 ; 4 . a2 / b sont des monômes
1. 3. 4. - POLYNÔMES
L'expression contient des signes d'addition ou de soustraction entre plusieurs monômes.
Exemple :
3x2y2 + 3 / 2 x2 - 4 (a2 / b) est un polynôme
![]() 2. - CALCULS
SUR LES MONÔMES
2. - CALCULS
SUR LES MONÔMES
2. 1. - ÉCRITURE D'UN MONÔME
Étant donné qu'un monôme est un produit de facteurs, et que l'on peut intervertir l'ordre de ses facteurs, sans changer le résultat, il faut toujours s'arranger pour réduire les monômes sous une forme condensée plus facilement utilisable :
Exemple :
3 . a . 5 . 2 . b . y2
3 . 5 . 2 . a . b . y2 = 30aby2
Un monôme est composé de deux partie :
-
Un facteur numérique que l'on appelle coefficient ;
-
Un produit de facteurs littéraux que l'on appelle partie littérale.
Exemples :
3a2b 3 est le coefficient et a2b est la partie littérale ;
a2b 1 est le coefficient et a2b est la partie littérale ;
- a2b - 1 est le coefficient et a2b est la partie littérale.
(Pour les deux dernières expressions, le coefficient 1 est sous-entendu).
2. 2. - DEGRÉ D'UN MONÔME ENTIER
2. 2. 1. - DEGRÉ D'UN MONÔME PAR RAPPORT A UNE LETTRE
Définition : On appelle degré d'un monôme par rapport à une lettre, l'exposant de cette lettre dans ce monôme.
3a2b est de degré 2 pour (a) et de degré 1 pour b.
x3y4 est de degré 3 pour (x) et de degré 4 pour y.
2. 2. 2 . - DEGRÉ D'UN MONÔME PAR RAPPORT A UN ENSEMBLE DE LETTRES
Définition : On appelle degré d'un monôme par rapport à l'ensemble des lettres, la somme des exposants de toutes ses lettres.
Le monôme 2a2bx3y4 est de degré 10 (2 + 1 + 3 + 4) pour l'ensemble de ses lettres.
2. 3. - MONÔMES SEMBLABLES
Définition : Des monômes semblables sont des monômes qui ont même partie littérale.
Exemples :
3a2b ; 4a2b ; - 8a2b sont des monômes semblables
Il en découle tout de suite que la somme de plusieurs monômes semblables est un monôme semblable dont le coefficient est la somme des coefficients des monômes :
3a2b + 4a2b - 8a2b = (3 + 4 - 8) . a2b = - a2b
C'est ce que l'on appelle réduire les monômes semblables.
2. 4. - OPÉRATIONS SUR LES MONÔMES
2. 4. 1. - PRODUIT DE PLUSIEURS MONÔMES
Le produit de plusieurs monômes est un monôme :
- dont le coefficient est le produit des coefficients des monômes donnés ;
- dont la partie littérale comprend les lettres contenues dans les monômes, chacune d'elles étant affectée d'un exposant égal à la somme de ses exposants dans les facteurs.
Exemple :
3a2b . 4b2c . - 5bd = - 60a2b4cd
Coefficient : (3) . (4) . (- 5) = - 60
Degré pour a : 2
Degré pour b : 1 + 2 + 1 = 4
degré pour c : 1
degré pour d : 1
Pour l'ensemble : 2 + 4 + 1 + 1 = 8
2. 4. 2. - QUOTIENT DE MONÔMES
Le quotient d'un monôme par un monôme s'écrit sous la forme d'une fraction qu'il faut simplifier au maximum.
exemples :
3a2b : 4b2c = 3a2b / 4b2c = 3a2 / 4bc
On a simplifié numérateur et dénominateur par le terme commun b.
4ab2c3 : 2a2b2c2 = 4ab2c3 / 2a2b2c2 = 2 (c / a)
On a simplifié numérateur et dénominateur par 2ab2c2.
Remarque : Un monôme A est divisible par un nombre B, lorsque A contient toutes les lettres de B avec des exposants aux moins égaux.
Exemples :
- 15a2b3c4 / - 5ab3c2 = 3ac2 ; 5x3y2z4 / 6x3z3 = 5 / 6 . y2z
![]() 3. - CALCULS SUR LES POLYNÔMES
3. - CALCULS SUR LES POLYNÔMES
3. 1. - DÉFINITIONS
3. 1. 1. - POLYNÔME
Un polynôme est une somme de plusieurs monômes qui sont les termes du polynôme.
Exemples :
3ac2 + bc3 + 4 ; 2 / 5 . x2 + 3ax2 - 2 / 3 . x
3. 1. 2. - BINÔME
On appelle binôme, un polynôme qui ne contient que deux termes.
Exemple : 3a + 4b
3. 1. 3. - TRINÔME
On appelle trinôme, un polynôme qui ne contient que trois termes.
Exemple : 2x2 - 3xy + 4y2
3. 2. - RÉDUCTION DE POLYNÔMES
Il faut toujours commencer par rendre le polynôme le plus simple possible.
Exemple :
3x3 + 5x2y + 2xy2 + 2x3 - 4x2y + 2xy2
En réduisant, on trouve :
3x3 + 2x3 = 5x3
5x2y - 4x2y = x2y
2xy2 + 2xy2 = 4xy2
Le polynôme réduit s'écrira donc : 5x3 + x2y + 4xy2 dont la forme est quand-même plus simple que celle proposée ci-dessus.
Remarque : Il est de règle d'écrire un polynôme de manière que les degrés de ses termes, par rapport à une de ses lettres, aillent soit en diminuant, soit en augmentant.
Exemples :
- 8ax3 + 6bx2 + 3cx est ordonné par rapport aux puissances décroissantes de x.
- 3 + 2xy + (4 / 3) . xy2 - 6y3 est ordonné par rapport aux puissances croissantes de y.
D'autre part, on peut ordonner un polynôme (ou un monôme) en fonction de l'ordre alphabétique de ses lettres.
Exemples :
Au lieu de : 3ayx + 4yxz - 3bac
On écrira : 3axy + 4xyz - 3abc
et mieux : - 3abc + 3axy + 4xyz
3. 3. - DEGRÉ D'UN POLYNÔME
Définition : Le degré d'un polynôme par rapport à une lettre est l'exposant le plus élevé de cette lettre dans le polynôme.
3. 3. 1. - POLYNÔME A UNE SEULE LETTRE
Exemples :
2a + 3 est un binôme de premier degré en a ;
3a2 + 2a - 4 est un trinôme de second degré en a ;
8x2 - 3 est un binôme de second degré en x.
3. 3. 2. - POLYNÔME A PLUSIEURS LETTRES
Exemples :
x4 - 2xy3 est de degré 4 pour x et 3 pour y.
3. 4. - OPÉRATIONS SUR LES POLYNÔMES
3. 4. 1. - ADDITION DE POLYNÔMES
Règle : La somme de plusieurs polynômes s'obtient en écrivant les termes des polynômes les uns à la suite des autres et en réduisant les termes semblables du polynôme obtenu.
Exemple :
(x4 + 3x2y2 + 3y) + (3x4 + 2x2y3 + 5y) = x4 + 3x2y2 + 3y + 3x4 + 2x2y3 + 5y = x4 + 3x2y2 + 2x2y3 + 8y
3. 4. 2. - SOUSTRACTION DE POLYNÔMES
Règle : Pour retrancher un polynôme, on ajoute les termes de ce polynôme changés de signe.
Exemples :
1) (x4 + 3x2y) - (2x4 - 4x2y) = x4 + 3x2y - 2x4 + 4x2y = - x4 + 7x2y
2) (3ab2 + 2a2b) - (2ab2 + 2a2b) = 3ab2 + 2a2b - 2ab2 - 2a2b = ab2
3. 4. 3. - PRODUIT D'UN POLYNÔME PAR UN MONÔME
Règle : Pour multiplier un polynôme par un monôme, on multiplie successivement chaque terme du polynôme par le monôme. C'est le produit d'une somme par un nombre.
Exemple :
(2x3 - x2 + 2) . (3xy) = 6x4y - 3x3y + 6xy
3. 4. 4. - PRODUIT D'UN POLYNÔME PAR UN POLYNÔME
Un polynôme étant la somme de plusieurs monômes, on appliquera la règle de la multiplication d'une somme par une somme.
Règle : Pour multiplier deux polynômes entre eux, on multiplie chaque terme de l'un successivement par chaque terme de l'autre et on ajoute algébriquement les produits obtenus. Ensuite on réduit les termes semblables.
Exemple :
(2ab - 3a + b) . (ab + 2a - b) =
|
2a2b2 - 3a2b + ab2 |
+ 4a2b - 6a2 + 2ab |
- 2ab2 + 3ab - b2 |
|
Produit par ab |
Produit par 2a |
Produit par - b |
Et en réduisant : 2a2b2 + a2b - ab2 - 6a2 + 5ab - b2
3. 4. 5. - PRODUITS REMARQUABLES
Il y a quelques produits remarquables qu'il est souhaitable de connaître par cœur.
Carré de la somme de deux nombres :
(a + b)2 = (a + b) (a + b) = a2 + 2ab + b2
Carré de la différence de deux nombres :
(a - b)2 = (a - b) (a - b) = a2 - 2ab + b2
Produit de la somme de deux nombres par leur différence :
(a + b) (a - b) = a2 - b2
D'autres produits remarquables sont importants :
(a - b) (a2 + ab + b2) = a3 - b3
et
(a + b) (a2 - ab + b2) = a3 + b3
ainsi que
(a + b)3 = a3 + 3a2b + 3ab2 + b3
et
(a - b)3 = a3 - 3a2b + 3ab2 + b3
Remarque : L'utilisation des produits remarquables conduit souvent à la décomposition d'un polynôme en produits de facteurs plus simples qui sont susceptibles de réductions ultérieures.
Prenons un exemple, soit :
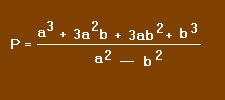
Le numérateur et le dénominateur sont des produits remarquables. Nous pouvons donc écrire :
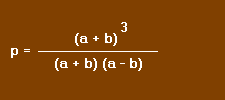
et en simplifiant par a + b nous trouvons :
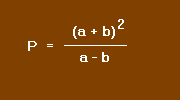
Expression plus simple que celle proposée.
3. 4. 6. - DIVISION D'UN POLYNÔME PAR UN MONÔME
Le quotient du polynôme P = 10x3 - 4x2y + 6xy2 par le monôme 2x est le polynôme qu'il faut multiplier par 2x pour obtenir le polynôme P. On écrit :
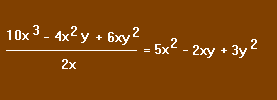
Un polynôme est donc divisible par un monôme lorsque tous les termes de ce polynôme sont divisibles par ce monôme.
Règle : Pour diviser un polynôme par un monôme, on divise tous les termes de ce polynôme par le monôme.
Application :
1 - Mise en facteur commun.
Considérons le polynôme :
25ax4 + 35ay4 - 55ax2y2
Tous ses termes étant divisibles par 5a, on peut l'écrire sous la forme :
5a (5x4 + 7y4 - 11x2y2)
On dit que le monôme (5a) a été mis en facteur commun dans le polynôme.
Le monôme de plus haut degré pouvant être mis en facteur dans un polynôme comprend les lettres communes à tous les termes, chaque lettre étant affectée du plus petit exposant qu'elle a dans le polynôme. Le coefficient du monôme mis en facteur peut être arbitraire (exemple 1), mais on prend le plus souvent pour coefficient le plus grand commun diviseur des coefficients des termes (exemple 2).
Exemple 1 :
18x3y - 11x2y2 + 22xy3 = x (18x2y - 11xy2 + 22y3)
Nous avons pris (x) comme facteur commun, alors que nous aurions pu prendre xy.
Exemple 2 :
12x2y3 + 15x3y2 = 3x2y2 (4y + 5x)
2 - Décomposition d'un polynôme en un produit de facteurs.
Cette décomposition est possible :
a - mettant un monôme en facteur commun
b - en groupant les termes du polynôme de manière à pouvoir effectuer ensuite des mises en facteur commun.
Exemple :
ab + bx + ay + xy = (ab + bx) + (ay + xy)
Mettons (b) en facteur commun dans la première somme et (y) en facteur commun dans la seconde :
b (a + x) + y (a + x)
Mettons (a + x) en facteur :
(a + x) (b + y)
c - en appliquant les propriétés des produits remarquables.
Exemple 1 :
4x2 + 20x + 25 = (2x + 5)2 ; application de (a + b)2
Exemple 2 :
18abx2 - 12abx + 2ab = 2ab (9x2 - 6x + 1) = 2ab (3x - 1)2 ; application de (a - b)2
Exemple 3 :
x2 + y2 - z2 + 2xy = (x2 + y2 + 2xy) - z2
= (x + y)2 - z2 ; application de (a + b)2
= (x + y + z) (x + y - z) ; application de (a + b) (a - b)
La décomposition des polynômes en produits de facteurs est souvent appliquée à la simplification des fractions.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente
|
 Page suivante Page suivante |
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.
 Calculs sur les monômes
Calculs sur les monômes
