Les Fractions et les Rapports :
MATHÉMATIQUES "3ème Partie"
5. - LES FRACTIONS
5. 1 - GÉNÉRALITÉS
Un objet quelconque peut être divisé (ou fractionné) en un certain nombre de morceaux.
Par exemple, une galette peut être découpée en un certain nombre de parts. Chaque part est une fraction de la galette.
Le mètre a été divisé en un certain nombre de "morceaux". Ces "morceaux" sont des fractions du mètre : le décimètre, le centimètre, le millimètre.
5. 2. - REPRÉSENTATION DES FRACTIONS
Si nous coupons, ou fractionnons, la galette en 8 parts égales et que nous en prenons une, on dira que nous avons pris un huitième de galette, et cette fraction de galette s'écrira en chiffre : 1 / 8
Cette notation rappelle de la division : numérateur - dénominateur.
Le chiffre au-dessus de la barre de fraction est appelé numérateur, celui qui est au-dessous est appelé dénominateur.
Le dénominateur indique en combien de fractions égales on a divisé, fractionné un ensemble. Le numérateur indique combien de fractions que l'on considère.

Une règle mesure 30 centimètres. Cela veut dire que l'on a divisé le mètre en 100 parties égales (on a obtenu des centimètres) et que la longueur de la règle est égale à 30 de ces parties égales.
Longueur de la règle = 1 mètre / 100 x 30 = 1 / 100 x 30
Le numérateur et le dénominateur sont les termes de la fraction.
Nous allons maintenant énoncer les différentes règles qui régissent les opérations sur les fractions. Nous vous invitons à les retenir (notamment pour les enfants).
5. 3. 1. - MULTIPLICATION
Règle : Pour multiplier 2 ou plusieurs fractions entre elles, on multiplie les numérateurs entre eux, et les dénominateurs entre eux.
Exemple :
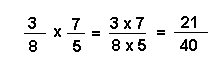
5. 3. 2. - DIVISION
Règle : Pour diviser deux fractions entre elles, on multiplie la fraction dividende par la fraction diviseur inversée.
Exemple :
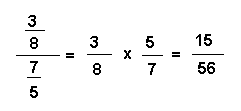
Remarque : Si le numérateur et le dénominateur de la fraction dividende sont divisibles respectivement par le numérateur et le dénominateur de la fraction diviseur, on divise les numérateurs entre eux et les dénominateurs entre eux.
Exemple :
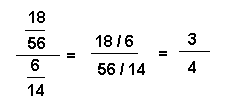
5. 3. 3. - ADDITION
Règle : Pour additionner plusieurs fractions entre elles, il faut :
- Les réduire au même dénominateur ;
- Additionner les numérateurs entre eux ;
- Garder le dénominateur commun.
Exemple :
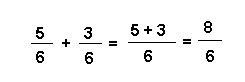
Réduction au même dénominateur : Pour réduire deux fractions au même dénominateur, on multiplie les deux termes de la première par le dénominateur de la seconde et les deux termes de la seconde par le dénominateur de la première.
Exemple :
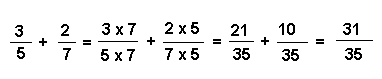
S'il y a plus de deux fractions, on peut procéder par étapes successives.
Exemple :
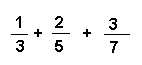
1 - On considère les deux premières fractions suivantes :
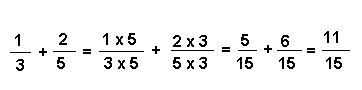
2 - On considère maintenant cette nouvelle fraction avec la 3ème.
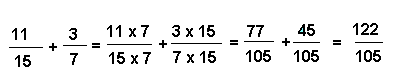
et, éventuellement, ainsi de suite.
Remarques : Il y aura lieu de simplifier les fractions chaque fois que cela sera possible, c'est-à-dire avant, pendant et après les calculs.
On simplifie une fraction en divisant chacun de ses deux termes par un même nombre. La nouvelle fraction obtenue est égale à la première.
Exemple :
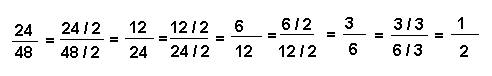
Il est bien évident que l'on n'est pas obligé de passer par tous les calculs intermédiaires. Il faut essayer de trouver le plus grand commun diviseur des deux nombres.
Exemple :

On voit immédiatement que 27 est divisible par 3 ainsi que 36. Mais on s'aperçoit aussi que ces deux nombres sont divisibles par 9 ; d'où :
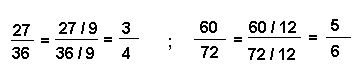
Nous venons de voir qu'on ne change pas la valeur d'une fraction en divisant ses deux termes par le même nombre. Ceci est aussi vrai pour la multiplication de ces deux termes, mais toujours par un même nombre non nul.
Exemple :
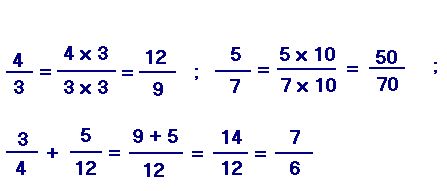
D'où la règle : On ne change pas la valeur d'une fraction en multipliant ou en divisant chacun de ses termes par un même nombre non nul.
2 - On peut, pour simplifier l'écriture lors de la réduction au même dénominateur, ne pas poser tous les calculs comme on l'a fait mais effectuer les opérations mentalement.
Dans l'exemple qui suit, les flèches indiquent les produits à effectuer.
Exemple :
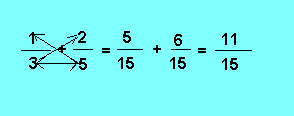
D'autre part, puisque l'on sait que le dénominateur sera le même pour les deux fractions, on peut ne l'inscrire qu'une seule fois, ce qui devient :
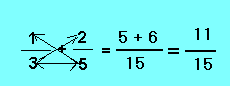
5. 3. 4. - SOUSTRACTION
Règle : Pour retrancher deux fractions entre elles, il faut :
1) Les réduire au même dénominateur ;
2) Soustraire les numérateurs ;
3) Garder le dénominateur commun.
Dans l'exemple qui suit nous allons, pour alléger l'écriture, procéder comme il vient d'être dit dans la remarque précédente :
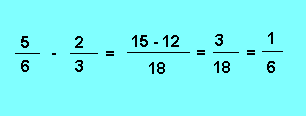
5. 3. 5. - PUISSANCES
Règle : Pour élever une fraction à une puissance, on élève chaque terme de la fraction à la puissance (on devrait dire "exposant").
Exemple :
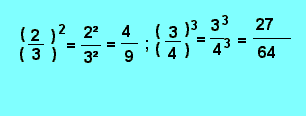
5. 3. 6. - RACINES
Règle : la racine d'une fraction est égale à la racine de chacun de ses termes.
Exemple :
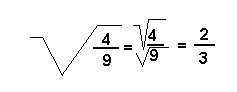
![]() 5.
4. - OPÉRATIONS
SUR LES FRACTIONS ET LES NOMBRES ENTIERS
5.
4. - OPÉRATIONS
SUR LES FRACTIONS ET LES NOMBRES ENTIERS
5. 4. 1 - Multiplication
règle : Pour multiplier une fraction par un nombre (ou un nombre par une fraction), on multiplie le numérateur par ce nombre ou on divise le dénominateur par ce nombre.
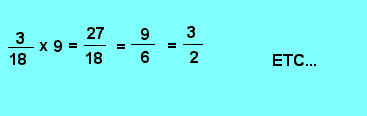
5. 4. 2. - TRANSFORMATION D'UNE FRACTION EN NOMBRE ENTIER (OU DÉCIMAL) ET INVERSEMENT
Comme il a été dit, une fraction se présente sous la forme d'un quotient. Si l'on effectue ce quotient, on obtient un nombre entier ou décimal égal à la fraction.
exemple :
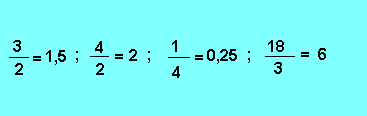
Remarque : Dans le cas où le résultat du quotient est un nombre entier, la fraction est aussi appelée rapport. Si au contraire, nous avons un nombre entier, ou décimal, à convertir en fraction nous opérerons ainsi :
1 - Nombre entier : il faut multiplier ce nombre par le dénominateur souhaité.
Exemples : On désire transformer le chiffre 3 en un certain nombre de tiers, quart, cinquième, etc...
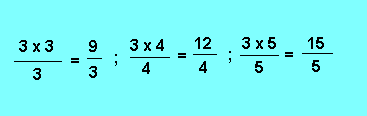
2. - Nombre décimal : Il faut multiplier ce nombre par la puissance de 10 qui transformera le nombre décimal en nombre entier.
Exemples :
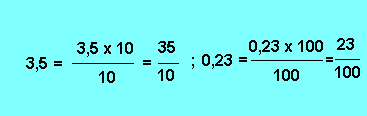
5. 5. - NOMBRE FRACTIONNAIRE
Les opérations ci-dessus sont dédiés aux enfants et à ceux qu'ils veulent à apprendre ainsi que les adultes comme ci-après.
Définition : Un nombre fractionnaire est un nombre entier suivi d'une fraction.
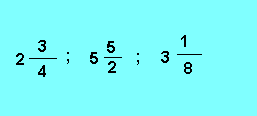
On peut convertir ces nombres fractionnaires en nombres décimaux.
Exemples :
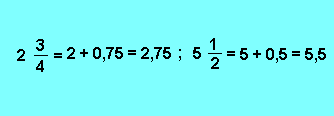
On peut également convertir les nombres fractionnaires en fraction.
Exemples :
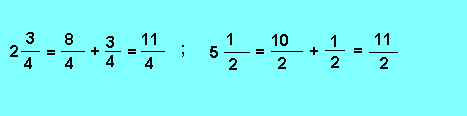
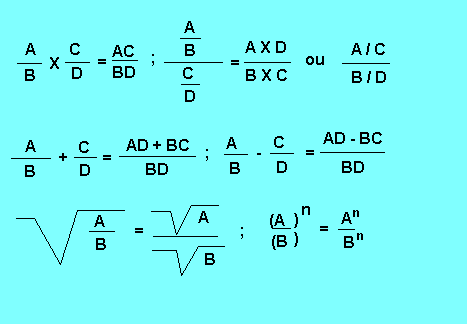
Résumé :
![]() 6. - RAPPORTS
6. - RAPPORTS
Définition : On appelle rapport de deux nombres "a" et "b" la quotient exact de ces deux nombres.
C'est ce que nous avions vu en examinant les fractions.
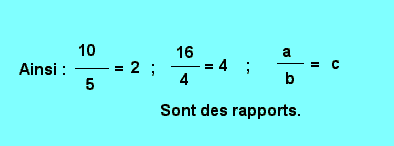
On définit également le rapport de deux nombres comme étant le nombre par lequel il faut multiplier le second pour obtenir le premier.
Ainsi de a / b = c, on peut écrire c x b = a. Cela est maintenant évident. En effet, nous reconnaissons la manière d'effectuer la preuve de la division.

6. 1. - PROPRIÉTÉS DES RAPPORTS
Comme un rapport s'exprime sous la forme d'une fraction, les règles examinées au sujet des fractions s'appliquent toutes aux rapports, et en particulier les sommes, produits et quotients.
Un rapport est donc assujetti aux mêmes règles et susceptible des mêmes simplifications qu'une fraction.
Dans l'étude des propriétés qui suit, nous rappellerons simplement celles que nous avons déjà vues avec les fractions.
Première propriété : On ne change pas la valeur d'un rapport en multipliant ou en divisant ses deux termes par un même nombre :
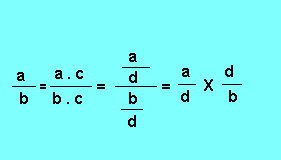
Deuxième propriété : Pour additionner deux ou plusieurs rapports, on les réduit au même dénominateur, puis on additionne les numérateurs et on conserve le dénominateur commun.
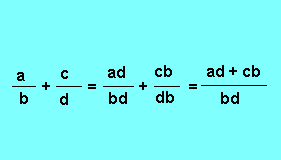
Troisième propriété : Pour multiplier entre eux deux ou plusieurs rapports, on multiplie les numérateurs entre eux et les dénominateurs entre eux :
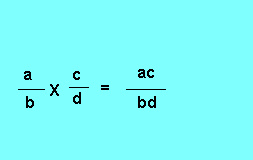
Quatrième propriété : Pour diviser deux rapports entre eux, on multiplie le rapport dividende par le rapport diviseur inversé :
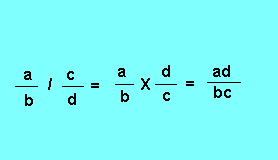
Cinquième propriété : Dans une suite de rapports égaux, le rapport obtenu, en prenant comme numérateur la somme des numérateurs, et comme dénominateur la somme des dénominateurs, est un rapport égal aux précédents.
Exemple :
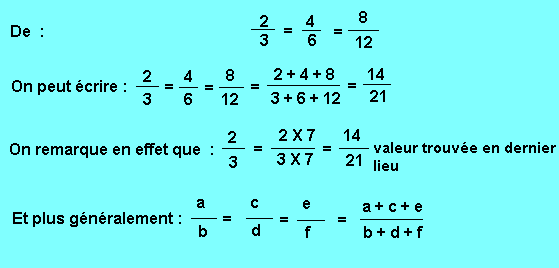
Sixième propriété : Dans une suite de rapports égaux, le rapport obtenu en prenant comme numérateur la différence des numérateurs, et comme dénominateur la différence des dénominateurs, est un rapport égal aux précédents.
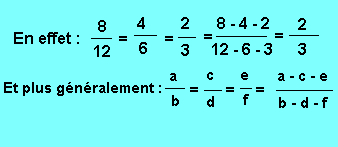
![]() 7. - PROPORTIONS
7. - PROPORTIONS
Définitions : On appelle proportion l'égalité de deux rapports.
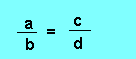
-
- a, b, c et d sont les termes de la proportion ;
-
- a et d sont les termes extrêmes, appelés plus simplement ("extrêmes") ;
-
- b et c sont les termes intermédiaires, appelés "moyens".
7. 1. - PROPRIÉTÉS DES PROPORTIONS
Première propriété : Dans une proportion, le produit des extrêmes est égal au produit des moyens. Soit :
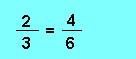
Nous voyons immédiatement que : 2 X 6 = 3 X 4
Et plus généralement :
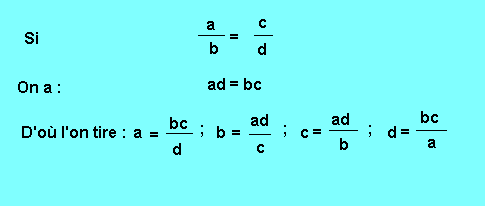
Deuxième propriété : Dans une proportion, on peut permuter :
![]() soit les extrêmes ;
soit les extrêmes ;
![]() soit les moyens ;
soit les moyens ;
![]() ou les extrêmes et les moyens.
ou les extrêmes et les moyens.
Reprenons l'égalité littérale trouvée précédemment :

Divisons les deux membres de cette égalité par le produit ab :

Divisons cette fois les deux membres par le produit cd :

Divisons enfin cette égalité par le produit ac :

Troisième propriété : Dans une proportion, on peut remplacer chaque rapport par son inverse :
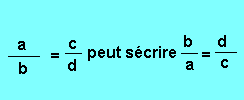
7. 2. - QUATRIÈME PROPORTIONNELLE
Définition : On appelle quatrième proportionnelle aux trois nombres a, b et c le nombre x tel que :
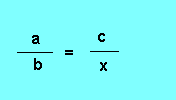
En faisant l'égalité entre le produit des extrêmes et des moyens, on trouve : ax = bc
Et, en divisant les deux termes par a :
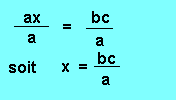
7. 3. - MOYENNE PROPORTIONNELLE
Définition : On dit que le nombre x est moyen proportionnel entre a et b. Si :
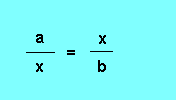
Faisons produit des extrêmes = produit des moyens :
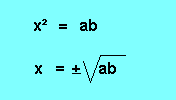
Remarques :
-
1) a et b sont tous deux positifs ou tous deux négatifs.
-
2) Le signe ± se lit "plus ou moins". Il est nécessaire dans notre exemple car un carré a toujours deux racines carrées opposées. En effet, (+2)² = 4 et (-2)² = 4 (Application de la règle des signes).
7. 4. - RÉCAPITULATION DES PROPRIÉTÉS DES RAPPORTS PROPORTIONS
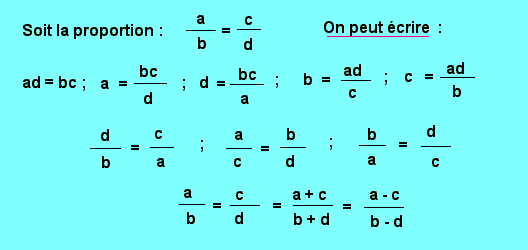
Pour bien comprendre les leçons d'électroniques, nous allons continuer les maths afin de comprendre et de connaître la représentation graphique.
Avec les graphiques, nous avons toutes les valeurs sous les yeux et le calcul se réduit à une simple observation, complétée tout au plus par quelques opérations graphiques.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente
|
 Page suivante Page suivante
|
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.
 Opérations sur les fractions
Opérations sur les fractions
