Les Puissances et les Racines :
MATHÉMATIQUES "2ème PARTIE"
3. - LES PUISSANCES
Nous abordons maintenant la deuxième partie de notre leçon.
Auparavant, nous vous conseillons, au fur et à mesure de votre lecture, de résoudre les exercices cités en exemples. Chacun des exercices terminés, comparez votre résultat à celui qui vous est donné. Quelques jours plus tard, recommencez cette fois sans regarder à priori le développement, mais comparez toujours les résultats.
Nous le répétons, en mathématiques, il faut pratiquer et répéter pour comprendre et retenir.
Poursuivons. Si nous considérons, comme nous l'avons dit, que les quatre opérations élémentaires (addition, soustraction, multiplication, division) sont connues du lecteur, il nous semble utile de parler de "l'élévation à une puissance" et de son inverse, c'est-à-dire de "l'extraction d'une racine". Les six opérations arithmétiques seront alors connues.
L'élévation à une puissance est une forme particulière de la multiplication.
Définition : On appelle puissance d'un nombre le produit de plusieurs nombres égaux entre eux.
Par exemple, le nombre 100, que l'on peut obtenir en multipliant 10 par 10 est une puissance de 10. Le nombre 1 000, que l'on peut obtenir en multipliant 10 par 10 et le résultat encore par 10, est une autre puissance de 10. Le nombre 16, que l'on peut obtenir en multipliant 2 par 2, le résultat par 2 et le nouveau résultat encore par 2, est une puissance de 2. Ce qui s'écrit : 10 . 10 = 100, 10 . 10 . 10 = 1000, 2 . 2 . 2 . 2 = 16.
Toutefois, dans les expressions mathématiques ordinaires, pour indiquer ces calculs, on a recours à une convention qui a l'avantage d'être très concise et de mettre en évidence les propriétés des puissances.
Comme les facteurs de la multiplication qui servent au calcul d'une puissance sont tous égaux, on écrit une seule fois le nombre servant de facteur puis on écrit à côté de celui-ci, en haut et à droite, le nombre qui représente la quantité de facteurs. En procédant ainsi, l'élévation à la puissance des exemples précédents s'écrira de la manière suivante :
102 = 100 ; 103 = 1 000 ; 24 = 16
Le nombre qui représente les facteurs égaux s'appelle la base (les nombres 10, 10 et 2 sont les bases des puissances respectives prises en considération). L'autre nombre, qui indique la quantité de ces mêmes facteurs s'appelle l'exposant (les nombres 2, 3 et 4, des exemples donnés sont des exposants).
L'ensemble base et exposant forme la puissance.
Lorsque l'exposant est 2, la puissance s'appelle le carré ou puissance deux. Lorsque l'exposant est 3, la puissance s'appelle le cube ou puissance trois. Avec les exposants 4, 5, 6... On dit respectivement puissance quatre, puissance cinq, puissance six, etc...
En rapport avec ces puissances, les opérations servant à en calculer les valeurs s'appellent respectivement élévation au carré, ou bien à la puissance deux, élévation au cube, ou bien à la puissance trois, élévation à la puissance quatre, à la puissance cinq, à la puissance six, etc... Notons que cette terminologie employée dans le langage courant n'est pas rigoureuse car on devrait dire : 10 exposant 2, 10 exposant 3, 2 exposant 4 au lieu de 10 puissance 2, 10 puissance 3, 2 puissance 4, etc...
Il peut être très utile d'écrire un nombre sous la forme d'élévation à une puissance pour obtenir des expressions arithmétiques abrégées, en particulier lorsqu'il s'agit de nombres très grands formés de peu de chiffres et suivis de beaucoup de zéros, ou bien dans les calculs de nombres très petits, formés de chiffres décimaux précédés de beaucoup de zéros.
Pour nous fixer les idées, considérons le cas d'une nombre très grand : cent milliards.
Sous la forme ordinaire, ce nombre s'écrit avec onze zéros après le chiffre 1, soit 100 000 000 000.
Évidemment, il est un peu fastidieux d'écrire un nombre aussi grand ; toutefois, si l'on considère que :
100 000 000 000 est égal 10 . 10 . 10 . 10 . 10 . 10 . 10 . 10 . 10 . 10 . 10
et que c'est donc une puissance de 10, nous pourrons après avoir compté le nombre de facteurs (qui est de 11, tout comme le nombre de zéros), écrire de façon plus concise 1011, au lieu d'aligner une longue file de zéros.
De façon analogue, en considérant que le nombre :
1 200 000 est égal à 12 . 10 . 10 . 10 . 10 . 10,
On pourra transformer en élévation à une puissance la partie de la multiplication qui suit le 12. Le résultat sera :
1 200 000 = 12 . 105
L'expression des nombres sous la forme d'élévation à une puissance, qui d'une façon très évidente est très utile pour abréger l'écriture, peut également entraîner une simplification notable des opérations arithmétiques, lorsqu'on doit effectuer des calculs avec deux ou plusieurs puissances.
Voyons brièvement les principales règles auxquelles obéissent les calculs des puissances.
Règle 1 : Le produit de deux ou plusieurs ayant la même base, est égal à une puissance ayant la même base et un exposant égal à la somme des exposants.
Exemples :
102 . 103 . 106 = 102 + 3 + 6 = 1011
53 . 52 . 51 = 53 + 2 + 1 = 56
Règle 2 : La division de deux puissances ayant la même base est égal à une puissance ayant la même base et un exposant égal à la différence des exposants.
Exemple :
74 / 72 = 74 - 2 = 72
Dans les applications de cette règle, on peut rencontrer trois cas particuliers que nous allons examiner.
CAS 1 : la différence des exposants est égal à 1.
Exemple :
34 / 33 = 34 - 3 = 31
L'exposant de la puissance qui constitue le résultat de l'opération est égal à 1. Dans ce cas particulier, on a donc 31 = 3, comme précédemment on avait 51 = 5. Donc, l'exposant 1 signifie qu'il n'y a qu'un facteur unique.
CAS 2 : la différence des exposants est égal à zéro.
Exemple :
112 / 112 = 112 - 2 = 110
Puisque 112 = 121, on a : 112 / 112 = 121 / 121 = 1
donc : 112 / 112 = 110 = 121 /121 = 1
La valeur qu'il faut attribuer à la puissance 110 est donc 1.
De la même manière, on trouve par exemple :
103 /103 = 100 = 1 000 / 1 000 = 1
0,52 / 0,52 = 0,50 = 0,5 x 0,5 / 0,5 x 0,5 = 0,25 / 0,25 = 1
Il est intéressant de remarquer que les puissances ayant un exposant égal à zéro ont toujours la même valeur : elles sont égales à 1, on aura donc :
20 = 1 ; 250 = 1 ; 10 0000 = 1 et ainsi de suite pour toute autre base ayant pour exposant zéro.
CAS 3 : la différence des exposants est égale à un nombre négatif.
Exemple :
72 / 75 = 72 - 5 = 7-3
Ce qui peut s'écrire :
72 / 75 = 7 . 7 / 7 . 7 . 7 . 7 . 7 = 7 . 7 . 1 / 7 . 7 . 7 . 7 . 7 = 1 / 7 . 7 . 7 = 1 / 73 = 1 / 343
La valeur de la puissance ayant un exposant négatif, 7-3 est donc égale à 1 / 343, soit 1 / 73
En conséquence, toute puissance ayant un exposant négatif est égale à une fraction ayant pour numérateur 1 et pour dénominateur cette même puissance dont l'exposant a été rendu positif.
On peut ainsi rendre positifs tous les exposants négatifs, par exemple :
10-1 = 1 / 101 = 0,1 ; 10-3 = 1 / 103 = 1 / 1 000 = 0,001 ; 10-6 = 1 / 1 000 000 = 0,000001
10-5 = 1 / 105 ; 45-13 = 1 / 4513 ; 1,31-4 = 1 / 1,314
Ou encore :
1 / 10-3 = 1 . 103 = 103 ; 4 / 8 . 10-2 = 4 / 8 . 102 = 1 / 2 . 102 = 0,5 . 102 = 50
Règle 3 : - Le produit de deux ou plusieurs puissances ayant le même exposant est égal à une puissance de même exposant ayant pour base le produit des bases.
102 x 52 = (10 x 5)2 = 502 = 2 500
Règle 4 : - La division de deux puissances ayant le même exposant est égale à une puissance dont l'exposant est le même et dont la base est égale au quotient des deux bases.
Exemples :
253 / 53 (25 : 5)3 = 53 ; 64 / 124 = (6 : 12)4 = 0,54 ; 15-1 / 3-1 = (15 : 3)-1 = 5-1 = 1 / 5
Règle 5 : La puissance de la puissance d'un nombre est la puissance de ce nombre dont l'exposant est le produit des deux exposants.
Exemple :
(32)3 = 32 x 3 = 36
Bien que les racines fassent l'objet du paragraphe suivant, nous donnons la règle suivante :
Règle 6 : La racine d'une puissance est égale à la base de cette puissance ayant pour exposant le quotient du premier exposant par la racine
Exemples :
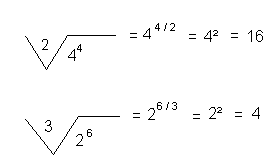
Nous donnons ci-après un tableau récapitulatif des opérations sur les puissances. Nous avons, par cette occasion, une application du calcul littéral.
TABLEAU RÉCAPITULATIF
am . an . ap = am + n + p
am / an = am - n si m > n
am / an = 1 / an - m si m < n
a1 = a
a0 = 1
am . bm . cm = (a . b . c)m
am / bm = (a / b) m
(am)n = am . n
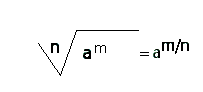
![]() 4. - LES RACINES
4. - LES RACINES
L'extraction de racine est l'opération inverse de l'élévation à la puissance. Comme il y a des puissances deux, trois, quatre... Il y a des racines deuxième ou carrée, troisième ou cubique, quatrième... Dans la pratique, c'est la racine carrée que l'on rencontre le plus souvent. C'est donc elle qui sera plus particulièrement traitée dans les lignes suivantes.
4. 1. - RACINE CARRÉE
Définition : La racine carrée d'un nombre A est le nombre B qui, multiplié deux fois par lui-même, sera égale à A.
Exemples :
La racine carrée de 9 est 3 car 3 x 3 = 9 ;
La racine carrée de 16 est 4 car 4 x 4 = 16 ;
La racine carrée de 25 est 5 car 5 x 5 = 25.
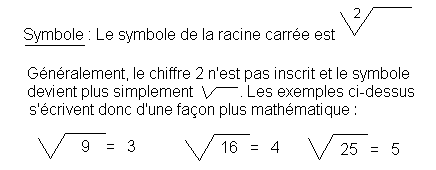
![]() 4.
2. - RACINE CUBIQUE
4.
2. - RACINE CUBIQUE
Définition : La racine cubique d'un nombre A est le nombre B qui, multiplié trois fois par lui-même, sera égal à A.
Exemples :
La racine cubique de 8 est 2 car 2 x 2 x 2 = 8
La racine cubique de 27 est 3 car 3 x 3 x 3 = 27
La racine cubique de 64 est 4 car 4 x 4 x 4 = 64
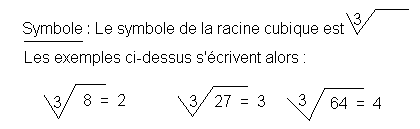
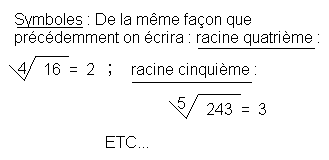
4. 3. - RACINE QUATRIÈME, CINQUIÈME
Définition : La racine quatrième (cinquième...) d'un nombre A est le nombre B qui, multiplié 4 fois (cinq fois...) par lui-même, sera égal à A.
Exemples :
Racine quatrième de 16 est 2 car 2 x 2 x 2 x 2 = 16
Racine cinquième de 243 est 3 car 3 x 3 x 3 x 3 x 3 = 243
4. 4. - EXTRACTION DE LA RACINE CARRÉE
Nous allons maintenant étudier la façon d'extraire une racine carrée. Cette opération demande une explication très détaillée. Mais lorsque vous aurez bien assimilé la procédure, vous verrez que l'extraction d'une racine carrée ne demande pas beaucoup plus de temps qu'une division.
Nous allons illustrer nos explications par un exemple ; Trouvez la racine carrée de 266,0161 :
Procédé :
1 - On écrit le nombre sous le radical (signe de l'opération consistant à extraire une racine).
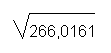
Comme on l'a dit, l'indice 2, qui devrait distinguer la racine carré des racines à indice supérieur (3, 4, 5...) est omis.
2 - On sépare le nombre donné "en tranches" de deux chiffres en partant de la droite vers la gauche, ou, s'il s'agit comme dans notre exemple d'un nombre décimal, en partant à droite et à gauche de la virgule.
2 . 66,01 . 61
Il peut arriver que le dernier groupe à gauche soit constitué d'un seul chiffre, comme le 2 de notre exemple. La même chose pourrait arriver au dernier groupe à droite de la virgule ; dans ce cas, il faut toujours ajouter un zéro, de façon qu'après la virgule tous les groupes soient formés de deux chiffres.
3 - Examinons le premier groupe à gauche, à savoir le 2. On calcule mentalement quel est le nombre entier qui, élevé au carré, permet d'obtenir le résultat le plus voisin, égal ou inférieur, au nombre formé par le premier groupe de chiffres.
Dans notre cas, ce nombre entier est 1, puisque le carré de 1, c'est-à-dire 1 x 1 est égal à 1 (tandis que le nombre entier suivant, soit 2, élevé au carré donne le résultat 4, qui est plus grand que 2). On écrit le nombre trouvé dans l'espace réservé pour la racine.
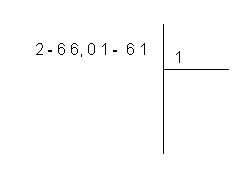
Si le nombre formé par les chiffres du premier groupe était 21, le nombre entier cherché serait quatre, parce que le carré 4 x 4 = 16 est inférieur à 21, tandis que le carré du nombre entier suivant, soit 5 x 5 = 25, est supérieur à 21. Par contre, si le nombre du premier groupe était 25, le nombre entier cherché serait 5, parce que 5 x 5 = 25.
4 - On reporte le carré du nombre entier trouvé précédemment sous le chiffre du premier groupe et l'on effectue la soustraction. Puisque le carré de 1 est égal à 1, sous le chiffre 2 on écrit 1 et on calcule la différence.
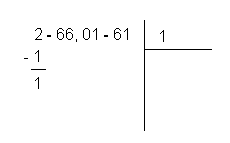
5 - A côté de la différence trouvée, on reporte les chiffres du second groupe, 66, et on sépare le dernier chiffre par un point.
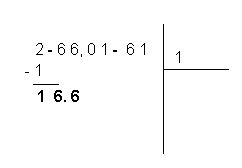
6 - On double le nombre présent dans l'espace réservé pour la racine (1 x 2 = 2) et on écrit sous la ligne horizontale le produit obtenu.
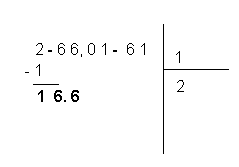
7 - On calcule mentalement le quotient entre le nombre 16, obtenu par la séparation du dernier chiffre du nombre 166, et le nombre 2, obtenu par le doublement du chiffre présent, dans l'espace réservé aux racines.
Puis on écrit le quotient à côté du 2, sous l'espace des racines. Enfin, on multiplie le nombre résultat par ce même quotient. Puisque 16 / 2 = 8, à côté du 2 on écrit ce nombre et on multiplie le nombre résultant (28) par 8.
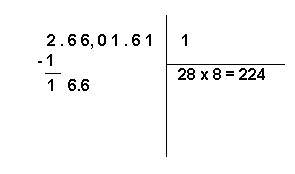
8 - On compare le produit 224 avec le nombre 166.
Le produit est plus grand que 166. On répète donc les opérations précédentes en diminuant le quotient d'une unité, c'est-à-dire, en utilisant le nombre 7 au lieu du nombre 8. Toutefois, même avec 7, le produit (189) est plus grand que 166. On répète donc les mêmes opérations avec le nombre inférieur à 7 soit avec 6.
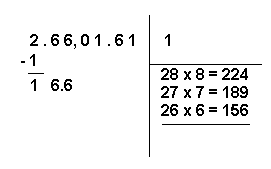
Le produit est inférieur à 166. On arrête donc cette série d'opérations en traçant une ligne horizontale sous la dernière multiplication.
9 - On écrit le produit 156 sous le nombre 166 et l'on effectue la soustraction. En outre, à côté de la différence on reporte le troisième groupe de chiffres, à savoir 01, en séparant le dernier chiffre par un point.
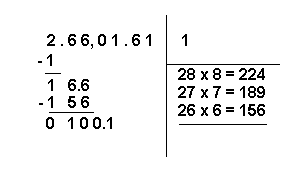
10 - On reporte 6 (à savoir le nombre qui nous a permis d'obtenir le produit 156 plus petit que 166) dans l'espace réservé à la racine, à côté du nombre 1.
Les deux chiffres forment le nombre 16. Le nombre 16 doit être doublé et le nouveau produit (16 x 2 = 32) doit être reporté sous les multiplications précédentes.
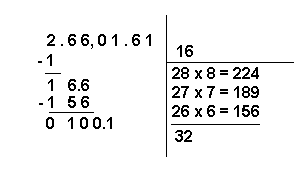
Après le chiffre 6, dans l'espace réservé à la racine, on met la virgule, puisque l'opération est terminée pour la partie entière du nombre 266, 0161.
11 - Maintenant, en répétant encore une fois le procédé commencé au point 7 (voir plus haut), on cherche le quotient de la division 100 / 32, en reportant seulement la partie entière du quotient. Ensuite, on écrit à côté de 32 le nombre qui représente la partie entière du quotient, à savoir 3 (100 / 32 = 3,...), et l'on effectue la multiplication par 3.
Puisque le produit obtenu (969) est inférieur à 1 001, on effectue immédiatement la soustraction entre les deux nombres. En outre, à côté de la différence on reporte le dernier groupe de chiffres, 61, en séparant par un point le dernier chiffre.
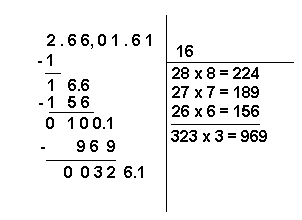
12 - On reporte le nombre 3 (à savoir le nombre qui nous a permis d'obtenir le produit 969, plus petit que 1 001) dans l'espace réservé pour la racine, immédiatement après la virgule. Ensuite, on double le nombre 163, obtenu en ajoutant 3 à la suite de 16 et en omettant la virgule, et l'on écrit le produit (163 x 2 = 326) sous la dernière multiplication.
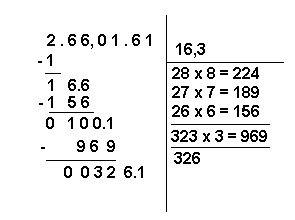
13 - Arrivez à ce point, examinons le nombre 326 obtenu en séparant le dernier chiffre de 3 261 et l'autre nombre 326, obtenu en doublant 16,3 et en supprimant la virgule.
La division de ces deux nombres 326 / 326 est égale à 1. Par conséquent, en suivant le procédé décrit aux points 7 et 11, on ajoute 1 à 326 et l'on multiplie par 1 le nombre ainsi formé. Le résultat de cette multiplication est soustrait de 3 261. Puisque le produit est lui aussi égal à 3 261, la différence sera égale à zéro.
On écrit le nombre 1, avec lequel on a effectué les précédentes opérations, à côté du dernier chiffre du nombre 16,3 dans l'espace réservé à la racine.

Le calcul est terminé (OUF !). Le résultat 16,31 est la racine carrée exacte du nombre 266,0161 puisque le reste est égal à zéro.
Pour vérifier ce résultat, il suffit de calculer le carré de la racine.
Dans notre cas, en effectuant la multiplication 16,31 x 16,31, on obtient 266,0161 qui est justement le nombre dont nous avons calculé la racine. Nous pouvons donc conclure que le résultat ne contient pas d'erreur.
Pour nous exercer, effectuons, sans en décrire toutes les opérations, le calcul de la racine carrée du nombre 179.
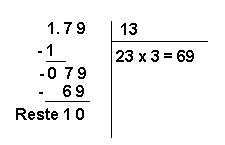
Le résultat obtenu est 13, mais puisque l'opération a un reste, 10, le nombre 13 n'est pas la racine carrée exacte de 179.
Dans des cas de ce genre, on peut poursuivre l'opération pour trouver d'autres décimales qui, ajoutées à la racine entière, forment un nombre aussi proche que possible de la valeur exacte de la racine.
A cette fin, on ajoute la virgule après le dernier chiffre du nombre dont on cherche la racine. Entre outre, après la virgule on ajoute un nombre de couples de zéros égal au nombre de décimales que l'on désire calculer pour la racine.
Par exemple, supposons que nous voulions calculer la racine carrée de 179, avec deux décimales. Dans ce cas, la virgule étant placée après le dernier chiffre, on ajoute deux couples de zéros. Puis on continue les calculs de la manière habituelle.
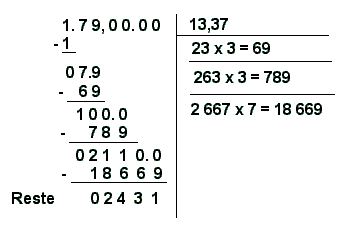
Le résultat 13,37 constitue la valeur approximative, calculée jusqu'à la deuxième décimale, de la racine carrée de 179. Pour effectuer la vérification de ce calcul, on procède comme dans le cas précédent, c'est-à-dire que l'on multiplie 13,37 x 13,37.
Le résultat de cette opération est 178,7569 ; comme on le voit, il n'est pas égal à 179, puisque le nombre 13,37 n'est que la valeur approchée de la racine. Pour compléter la vérification, il nous faut ajouter la valeur du reste :
178,7569 + 0,2431 = 179
Le résultat de cette dernière opération, en s'avérant égal au nombre donné au commencement des calculs, confirme l'exactitude de toutes les opérations.
Autre exemple avec une autre disposition : Calculez la racine carrée de 0,00027, nous écrivons :
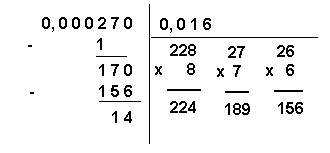
Comme le montre cet exemple, la partie entière du nombre est zéro, donc la partie entière de la racine est 0. Le premier groupe à droite de la virgule du nombre est constitué par deux zéros, donc, le premier chiffre décimal de la racine est zéro. Le second groupe à droite de la virgule est constitué par 02, ce qui revient à dire 2. Le plus grand carré contenu en 2 est 1 ; sa racine est 1, et celle-ci sera le second chiffre décimal de la racine cherchée.
L'extraction de la racine se poursuit normalement. Comme on l'a vu, l'extraction de la racine est une opération quelque peu fastidieuse.
D'autre part, même l'élévation au carré, qui est pourtant très simple, peut rendre fastidieux un calcul constitué par de nombreuses autres opérations ; on trouve maintenant dans le commerce à un prix raisonnable ou dérisoire, des machines à calculatrice scientifique permettant de trouver immédiatement la racine carrée ou le carré d'un nombre.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente
|
 Page suivante Page suivante
|
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.
 Les racines carrées
Les racines carrées
