Les Opérations dans les Machines Numériques :
7. - LES OPÉRATIONS DANS LES MACHINES NUMÉRIQUES
7. 1. - L'ADDITION DANS LES MACHINES NUMÉRIQUES
Au
chapitre 5. 2., nous avons vu le principe de l'addition binaire. Dans les systèmes numériques, il n'y a aucune différence et elle constitue l'opération
de base.
Elle est effectuée à partir de
cellules simples (opérateurs logiques) qui constituent les circuits de
logique combinatoire.
La table de l'addition binaire (figure
14) correspond à la table de vérité de l'opérateur
OU EXCLUSIF.
En binaire, si on effectue la somme
suivante : 1 + 1 = 10
Le chiffre le moins significatif (C.L.M.S.)
est un 0 (résultat correspondant à la
partie en cyan de la figure 14). Le chiffre le plus significatif (C.L.P.S.),
qui constitue le report est 1.
Le
C.L.M.S.
est donné par la sortie du circuit
OU exclusif,
tandis que le report, ou
C.L.P.S., est
fourni par la sortie du circuit
ET.
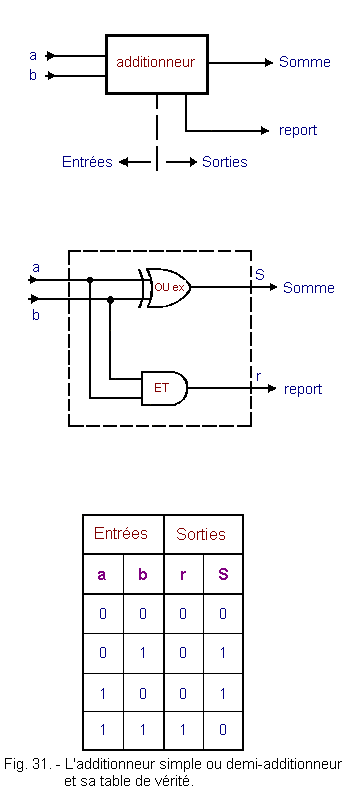
Le schéma de cet additionneur est
donné à la figure 31 ainsi que sa table de vérité. Il porte sur l'addition
de deux nombres de un bit.
Cette représentation suppose que
cet additionneur ne peut recevoir aucun report extérieur, résultant d'un calcul antérieur.
C'est rarement le cas et pour
banaliser les circuits, on envisage une entrée supplémentaire correspondant à
ce report.
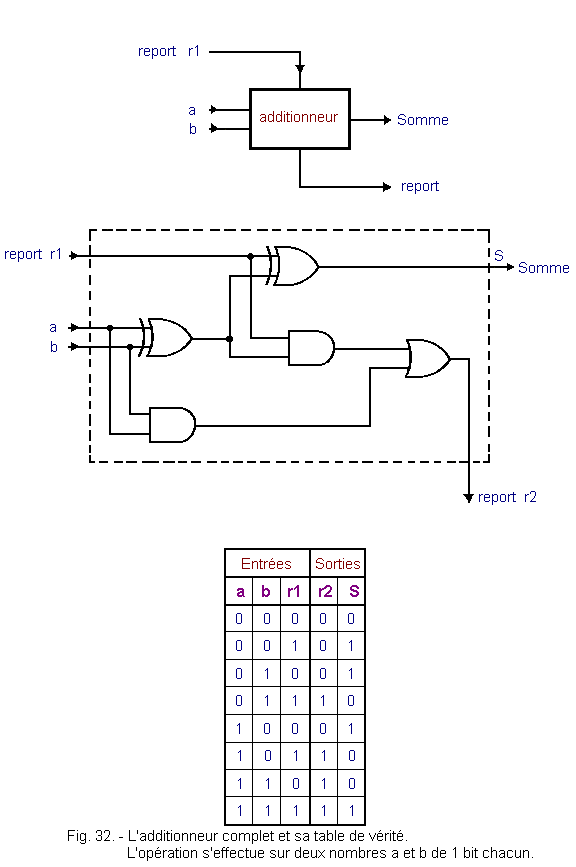
Le circuit devient celui de la
figure 32 avec sa table de vérité.
L'opération porte sur deux nombres
de un bit chacun.
Les nombres comportant plus de bits
sont additionnés de la même manière. Chaque additionneur verra sur ses entrées
des bits de poids identiques.
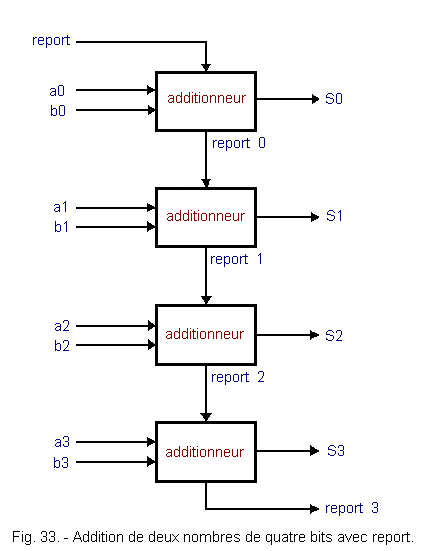
La figure 33 donne le schéma d'un additionneur portant sur deux nombres de quatre bits en binaire pur ou naturel. Le premier nombre étant formé des bits a0, a1, a2, a3 et le second nombre de b0, b1, b2, b3. Il n'est pas question ici de nombres signés, de précision multiple ou de virgule flottante.
Les additionneurs nécessitant une grande rapidité de fonctionnement sont conçus un peu différemment. Ils prennent l'appellation d'additionneurs à report anticipé par opposition à celui que nous venons de décrire où le report est à propagation série.
Sur ces additionneurs à report anticipé, celui-ci est recalculé pour chaque étage en fonction des éléments binaires précédents.
![]() 7. 2. - LA SOUSTRACTION
7. 2. - LA SOUSTRACTION
Nous avons écrit au début de ce chapitre qu'il serait intéressant d'utiliser une procédure universelle qui servirait à toutes les opérations. C'est un souhait qui faciliterait bien les choses. Puisque nous venons de décrire l'addition, voyons si ces circuits ne peuvent servir pour la soustraction.
Nous savons que le complément à 2 (que l'on représente par C2) est utilisé pour représenter les nombres négatifs.
Effectuer une soustraction revient à réaliser une addition dont le second terme est négatif.
De plus, il faut savoir que dans les systèmes numériques, les mots ont tous le même format. Ce format correspond à la longueur des registres.
Exemple :
Dans un système travaillant sur des mots de huit bits, le nombre décimal (+ 4) se trouve sous la forme : 0000 0100.
Le nombre décimal (- 9), dans la représentation des nombres négatifs par le C2, se trouve sous la forme : 1111 0111.
On entend, par même format, le fait que ces nombres utilisent pour leur représentation huit bits. Voyons ce qui se passe avec un exemple.
-
Soit à soustraire (+ 4) de (+ 9).
(+ 9) Þ 0000 1001
- (+ 4) devient (- 4) Þ 1111 1100
La figure 34 représente cette opération.
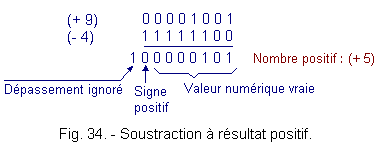
Le débordement ou dépassement est ignoré car il tombe en dehors de la capacité de stockage du registre qui ne comporte que huit cellules (donc huit éléments binaires : huit bits).
Le bit le plus significatif est un 0, comme il indique le signe de la valeur absolue, ce nombre est positif et, par conséquent, la valeur numérique trouvée correspond à celle du résultat.
Que se passe-t-il lorsque le second terme est, en valeur absolue, plus grand que le premier ?
Soit à soustraire (+ 9) de (+ 4), la figure 35 montre cette opération.
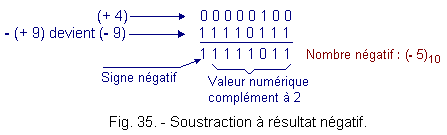
Le résultat donne un nombre ayant un 1 au B.L.P.S. (bit le plus significatif), donc une valeur négative.
Puisque nous avons opté pour la représentation des nombres par le complément à 2, si le signe est négatif, la valeur numérique qui suit ne peut être que le complément à 2 du nombre recherché.
Transformons en décimal :
11111011 Þ C2 Þ 00000101 Þ (- 5)10
Si ce résultat doit servir à d'autres calculs, il restera dans la machine sous forme de complément à 2.
Si ce résultat constitue la fin d'un calcul, avant de l'envoyer sur un afficheur afin de le visualiser (cas d'une calculette), il faudra effectuer le complément à 2 du résultat puis aiguiller celui-ci et le signe aux afficheurs correspondants.
Le complément à 2 et le signe négatif (-) sont liés l'un à l'autre.
Par exemple, si nous entrons, toujours dans le cas d'une calculette, un premier nombre, il sera stocké sous forme binaire.
Avant d'introduire le second nombre, nous indiquons le signe de l'opération. S'il s'agit d'une addition, le second terme sera stocké dans un second registre sous la même forme que le premier.
S'il s'agit d'une soustraction, le fait d'introduire le signe -, à l'aide du clavier, démarre la procédure de complémentation.
Une fois l'opération réalisée (après avoir appuyé sur la touche «=»), si le B.L.P.S. est un 1, la procédure de complémentation est engagée avant l'envoi du résultat vers l'affichage.
Mise à part la procédure de complémentation sur le second terme ou sur le résultat, nous utilisons pour la soustraction le même circuit additionneur que celui décrit figure 32.
La complémentation à 2 est obtenue à partir de l'information contenue dans le registre et sur laquelle on doit procéder à cette complémentation.
En général, ces registres ont deux sorties, l'une est la recopie du nombre précédemment entrée, l'autre correspond au complément à 1 de ce nombre (ces circuits vous seront décrits dans une leçon qui leur est consacré).
Cette seconde sortie est dirigée, le cas échéant, vers un additionneur. Dans celui-ci, au complément à 1, est ajouté 1 afin d'obtenir le complément à 2.
La figure 36 illustre cette méthode.
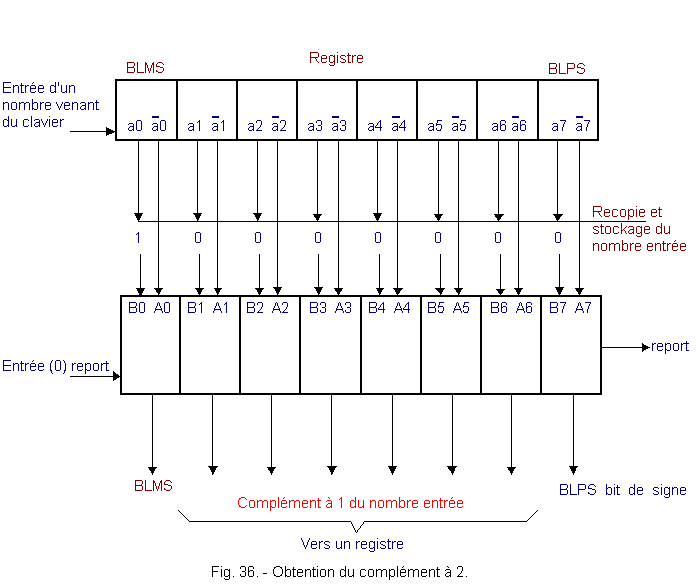
Pour l'instant, il n'est question que des principes utilisés dans les systèmes numériques pour effectuer les opérations.
Ces principes sont quelque peu différents des opérations arithmétiques de base, c'est pourquoi il faut y apporter des précisions, mais il n'est pas encore temps d'aborder la réalisation pratique et la description détaillée des schémas.
La sortie complément à 1 du registre est envoyée dans un additionneur. Dans ce dernier, on ajoute 1 au complément à 1 pour obtenir le complément à 2.
![]() 7. 3. - LA MULTIPLICATION
7. 3. - LA MULTIPLICATION
Les deux opérations qui vont suivre, multiplication et division, sont données à titre d'exemple, car la procédure pratique est quelquefois assez complexe et plusieurs méthodes sont utilisées. Toutefois, elles s'apparentent à celles décrites ci-dessous.
Nous savons, depuis le chapitre 5. 6. que la multiplication binaire est une suite d'additions dont les termes sont des recopies du multiplicande successivement décalés.
Là encore, nous constatons un point commun avec les deux opérations précédentes : l'addition.
Dans la soustraction, il est nécessaire d'effectuer, en plus de l'addition, le complément à 2.
Dans la multiplication, l'opération supplémentaire consiste en un décalage des résultats partiels avant l'addition.
Exemple : Soit à multiplier (+ 25) par (+ 5). Nous considérons que les nombres sont représentés dans la machine par des mots de huit bits et les valeurs négatives par le complément à 2.
_par_(+5)_en_binaire.gif)
La figure 37 montre le déroulement de cette multiplication.
.gif)
Le B.L.P.S. est 0, donc le nombre est positif et la valeur numérique représentée par les sept bits suivants correspond à la valeur absolue du résultat :
-
1111101 Þ |125|
Puisque le nombre est positif, le résultat est : (+ 125).
La partie correspondant au débordement est ignorée puisque le registre de stockage ne comporte que huit cellules élémentaires.
Voyons ce qui se passe si l'un des deux nombres est négatif :
Soit à multiplier (+ 25) par (- 5). La figure 38 représente cette nouvelle multiplication.
.gif)
Ici, l'opération a été volontairement poursuivie dans la partie débordement. Dans la pratique, cette partie de l'opération ne peut s'effectuer (à cause de la longueur des registres).
Le B.L.P.S. est à 1, par conséquent, il s'agit d'un nombre négatif et un tel nombre est représenté par son complément à 2.
Pour trouver la valeur absolue du résultat, il faut effectuer la complémentation à 2 (C2).
Soit : 10000011 Þ C2 Þ 01111101
La valeur absolue est |125|, le signe étant négatif, nous trouvons pour résultat : (- 125).
Avec deux exemples, on s'aperçoit que la notation, en virgule flottante et précision multiple est une nécessité car on est vite limité dans les calculs quand on ne travaille que sur des mots de huit bits ou octets.
En résumé, pour la multiplication, en commençant par le B.L.M.S. du multiplicateur, à chaque fois que l'on rencontre un 1, on recopie la multiplicande et on le décale d'autant de rangs vers les poids forts (vers la gauche) que le poids du bit multiplicateur.
Dans la pratique, on n'effectue pas la multiplication par 0. On gagne ainsi un cycle dans la procédure, ce qui se traduit par un léger gain de temps.
Le décalage vers les poids forts s'effectue aussi dans les registres. En fait, au lieu d'un blanc, comme dans l'exemple, chaque résultat partiel est stocké dans un registre et on pousse le contenu de celui-ci vers les poids forts en introduisant au B.L.M.S. un 0.
Les registres sont des circuits très important en électronique. Ils font partie des circuits dits : séquentiels.
Par ailleurs, le décalage vers les poids forts est utilisé, comme en décimal, pour la multiplication par une puissance de la base.
Exemple :
-
en décimal :
.gif)
-
en binaire : Soit à multiplier 0110 par 010.
0102 est une puissance entière de la base 2 (en décimal 0102 = + 2101).
La figure 39 montre cette multiplication.
.gif)
Dans cet exemple, nous avons effectué le produit par le 0 du B.L.M.S. Par contre, on ne l'a pas fait pour le 0 du B.L.P.S. ou bit de signe.
De plus, le décalage est ici d'un rang vers les poids forts puisque 102 Þ 2101. L'exposant de la puissance de 2 indique le décalage.
Nous aurions pu prendre à la place de 102, 10002, soit 2103. Le résultat est, dans ce cas :
0110 x 01000 = 0110000
Le décalage est ici de trois rangs vers les puissances supérieures.
![]() 7. 4. - LA DIVISION
7. 4. - LA DIVISION
Étant donné qu'elle constitue l'opération arithmétique la plus délicate, la procédure utilisée dans la machine ne la simplifie pas pour autant.
Il est bon d'en connaître le mécanisme. Toutefois, si ce dernier n'est pas très bien assimilé, cela n'entraîne pas de conséquences fâcheuses pour la suite du programme. Il sera toujours temps de revenir sur ce sujet quand bon vous semblera.
Nous utilisons pour cette opération, l'additionneur, le complément à 2 (addition et complément à 2 = soustraction), le décalage, la recherche du rang occupé par le bit à 1 de poids le plus élevé du diviseur, le test du bit de signe, la comparaison de grandeur numérique et, bien sûr, la mémorisation ou stockage.
Nous allons porter notre exemple sur la division suivante :
010101 / 011
Ces nombres, une fois stockés dans les registres à huit bits se présentent sous la forme suivante :
-
00010101 - dividende
-
00000011 - diviseur
Le signe de l'opération, ou opérateur, est aussi stocké dans un registre, spécialement destiné à cet effet, sous forme d'un mot binaire.
Pour cette opération, il y a une procédure préliminaire que l'on déclenche par l'introduction de cet opérateur et qui consiste à reconnaître le rang occupé par le bit à 1 de poids le plus élevé de la valeur absolue du diviseur.
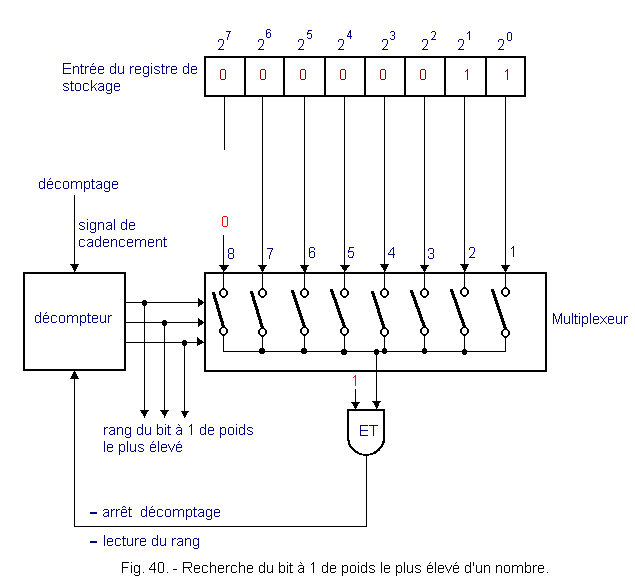
Cette opération peut s'effectuer selon le principe illustré figure 40 et que nous allons décrire.
On y reconnaît le registre de stockage qui nous est familier, suivi d'un multiplexeur commandé par un décompteur et un opérateur ET que vous connaissez.
Le multiplexeur et le décompteur seront décrits, en détail dans les théories suivantes. Sachez, pour l'instant que le multiplexeur est un circuit dans lequel chaque entrée est réunie à la sortie commune par un interrupteur (transistor bipolaire ou MOS).
La fermeture de chacun de ces interrupteurs est obtenue par une information binaire, présente à l'entrée du multiplexeur.
Cette information ne peut commander qu'un seul interrupteur à la fois.
L'information binaire est obtenue, dans notre cas, par un décompteur.
Le rythme de décomptage est obtenu par un signal de cadencement appliqué sur une entrée du décompteur.
Ce circuit possède une seconde entrée, branchée à la sortie de l'opérateur ET, qui stoppe le décomptage dès que celle-ci passe au niveau logique 1.
L'information en sortie du décompteur se présente sous la forme d'un nombre à n bits ; dans ce cas, trois bits suffisent car nous décomptons du 7ème rang au 1er rang (de 1112 à 0012). Ce nombre est codé sous forme binaire naturel tel que le montre la figure 41.

Dès que l'entrée «arrêt décomptage» passe à 1, le décompte est stoppé, et la lecture de l'information binaire, présente en sortie du décompteur indique le rang du bit à 1 de poids le plus élevé de la valeur absolue du diviseur. Le huitième rang, qui correspond au signe de la valeur absolue, n'est pas pris en compte pour l'instant.
Cette information est mise en mémoire et l'opération de complémentation peut être effectuée, car le signe mémorisé dans le registre de l'opérateur (ici la division ; /) implique la recherche du complément à 2 du diviseur.
Sont désormais présents dans la machine :
-
Le dividende Þ 0001 0101
-
Le diviseur Þ 0000 0011
-
Le rang du bit à 1 de poids le plus élevé Þ 010
-
Le complément à 2 du diviseur Þ 1111 1101
Dans la division décimale, nous cherchons à savoir combien de fois le diviseur est contenu entièrement dans le nombre formé par autant de chiffres de poids les plus élevés, que le diviseur en contient.
Autrement dit, on soustrait le diviseur des poids les plus élevés du dividende. Nous effectuons cette opération mentalement, mais les circuits numériques ne peuvent procéder ainsi.
C'est la raison de cette recherche concernant le bit à 1 de poids le plus élevé du diviseur. Nous effectuons la soustraction par une addition du complément à 2 et si le bit de signe est un 1, le résultat est négatif, cela veut dire que le terme soustracteur a une valeur absolue plus grande que celle du terme soustrait. On en déduit que le soustracteur, dans ce cas, n'est pas contenu dans le nombre formé des poids les plus forts du dividende.
Nous sommes, par conséquent, obligés dans cette opération de compter avec le bit de signe.
L'opération précédente qui nous a permis de connaître le rang du bit à 1 de poids le plus élevé, ne tient pas compte du bit de signe.
A cet effet, à l'information binaire présente en sortie du décompteur, nous devons ajouter un rang.
Les informations présentes dans la machine sont :
-
Le dividende Þ 0001 0101
-
Le diviseur Þ 0000 0011
-
Le rang du bit à 1 de poids le plus élevé, augmenté d'un rang pour le signe Þ 011
-
Le complément à 2 du diviseur Þ 1111 1101
Bien entendu, le signe de l'opération reste présent lui aussi, dans le registre opérateur.
Désormais, nous pouvons commencer l'opération.
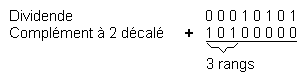
La disposition de l'opération nécessite une explication. Nous avons cherché le rang contenant le chiffre le plus significatif du diviseur, plus un rang pour le signe, afin de pouvoir soustraire le diviseur (dans notre cas, additionner son complément à 2), des chiffres de poids les plus élevés du dividende, pour savoir s'il est contenu entièrement dans ce dernier. Cette procédure nous permet de décaler le complément à 2, vers la gauche, afin de l'aligner sous le même nombre de rangs, de poids les plus élevés du dividende, qu'il en contient lui-même.
Revenons à l'opération.
La figure 42-a montre la première phase de l'opération.
a) 1ère phase :
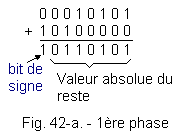
Il faut tester le bit de signe pour connaître le résultat de l'opération. Ceci est relativement facile à obtenir, il suffit, comme dans la figure 40, d'utiliser un opérateur logique ET sur lequel on envoie le bit de signe sur l'une de ses entrées et un 1 sur l'autre.
Dès que le bit de signe passe à 1, la sortie de l'opérateur ET prend l'état 1.
Quand cette sortie est à l'état 1, cela signifie que le diviseur n'est pas contenu dans le nombre formé par les chiffres de poids les plus élevés du dividende.
Dans ce cas, comme pour la division décimale, nous allons constituer un nouveau nombre avec un chiffre de rang supplémentaire au dividende.
Cela revient à décaler, vers la gauche, le dividende.
Le diviseur n'étant pas contenu dans les premiers termes de poids forts du dividende, le premier chiffre, de poids le plus élevé, du quotient partiel est : 0.
Après cette première phase, le quotient partiel se présente sous la forme :
0 . . . . . .
b) 2ème phase :
Le dividende est décalé une fois vers la gauche (figure 42-b).
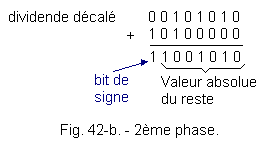
Le bit de signe du reste est à 1, donc le résultat est négatif, le diviseur n'est toujours pas contenu dans les termes de poids forts.
Le quotient partiel devient : 0 0 . . . . .
Nouveau décalage du dividende.
c) 3ème phase :
La figure 42-c montre l'opération après deux décalages à gauche du dividende.
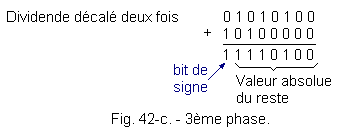
Résultat identique aux deux premières phases. Le bit de signe du reste est encore à 1.
Le nouveau quotient partiel est donc : 0 0 0 . . . .
d) 4ème phase :
Après un nouveau décalage à gauche, l'opération se présente comme le montre la figure 42-d.
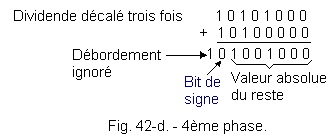
Là, le bit de signe est 0, ce qui signifie que le diviseur est contenu dans les termes de poids les plus élevés du dividende.
Le quotient partiel devient : 0 0 0 1 . . .
Les additions successives ne porteront plus sur le dividende mais sur le reste (comme en décimal), l'opération de décalage se poursuit sur la valeur absolue du reste.
Avant de continuer, il faut s'assurer que la valeur absolue du reste est supérieure à la valeur absolue du complément à 2 du diviseur. Ce circuit de comparaison vous est décrit un peu plus loin.
Donc si la valeur numérique absolue du reste est plus grande que celle du C2 du diviseur, l'opération se poursuit.
e) 5ème phase :
L'opération se poursuit donc avec, comme nouveau dividende, le reste précédent décalé une fois à gauche (figure 42-e).
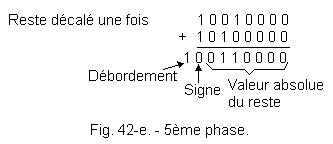
Le bit de signe est à 0, d'où le nouveau quotient partiel : 0 0 0 1 1 . .
Décalage vers la gauche, de la valeur absolue du reste.
Comparaison des grandeurs numériques.
Le reste est plus grand que le C2 du diviseur, l'opération se poursuit.
f) 6ème phase :
L'opération se poursuit avec le reste décalé deux fois vers la gauche (figure 42-f).
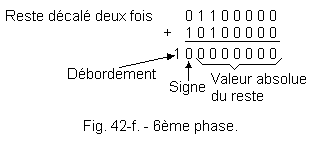
Le bit de signe est à 0, le nouveau quotient a pour valeur : 0 0 0 1 1 1 .
Décalage vers la gauche, de la valeur absolue du reste et comparaison des grandeurs numériques. La valeur absolue du reste décalé est inférieure à celle du complément à 2 du diviseur, l'opération s'arrête. Ici, la valeur absolue du reste est égale à 0, le quotient est exact et le dernier bit obtenu au quotient partiel constitue le B.L.M.S. du quotient (poids le plus faible).
Dans le registre de stockage du quotient, le résultat se présente sous la forme suivante : 0000 0111.
Lors de la dernière comparaison entre les valeurs absolues du reste et du C2 du diviseur, nous avions un résultat inférieur pour le reste et égal à 0.
Ce résultat aurait pu être inférieur, mais non égal à 0, et, dans ce cas, la division s'arrête, mais comporte un reste. Le quotient est alors un quotient approché.
La division portant sur des nombres fractionnaires est également possible, mais la notation en virgule flottante est préférable et facilite la procédure en ce qui concerne la position de la virgule.
La division est alors effectuée sur les mantisses et la valeur de l'exposant est trouvée en soustrayant celle du diviseur de celle du dividende.
En décimal, cela revient à l'exemple suivant :
Soit à diviser 0,125 par 3 :
-
0,125 = 0,125 x 100
-
3 = 0,3 x 101

Division effectuée sur les mantisses :
(+ 125) / (+ 3) =(+ 42)
Différence des exposants :
(0) - (+ 1) = (- 1)
Résultat en notation virgule flottante :
(+ 42) (- 1)
Transformation en décimal :
(+ 42) (- 1) = 0,42 x 10-1 = 0,042
Le principe que l'on vient de décrire retrace les grandes lignes de la division effectuée dans un système numérique, car les plus petits détails, consignés par écrit ou effectués mentalement, font quelquefois l'objet d'un assemblage complexe de circuits pour leur élaboration.
De plus, les constructeurs de machine à calculer et, d'une manière générale, ceux qui sont amenés à réaliser de tels circuits, qu'il s'agisse de logique câblée ou micro-programmée, utilisent des procédés qui leur sont propres, mais qu'ils divulguent rarement.
En tout cas, l'opérateur de base reste l'additionneur.
Les procédures nécessaires, à la bonne conduite du résultat, pour les opérations décrites sont :
-
la mémorisation
-
l'addition
-
la complémentation à 2
-
la recherche du rang occupé par le bit à 1 de poids le plus élevé d'un nombre
-
le test du bit de signe
-
la comparaison de grandeurs numériques.
Le test du bit de signe, à l'aide de l'opérateur ET nous permet, en inversant (c'est-à-dire en prenant le complément à 1), le résultat disponible en sortie de l'opérateur, d'extraire la valeur absolue du quotient. C'est donc la sortie inversée de l'opérateur ET qui servira à charger la valeur absolue du quotient dans le registre destiné à cet usage.
Nous avons, au cours de ces descriptions, parlé de débordement ignoré. En fait, ce débordement n'est pas toujours ignoré, il est même parfois stocké dans un registre et sert, entre autre, à indiquer un dépassement de capacité. Dans les microprocesseurs, un registre spécial appelé registre d'état, regroupe un certain nombre d'indications de ce genre que l'on peut tester à tout moment afin de donner une orientation différente aux procédures suivantes en cas de besoin.
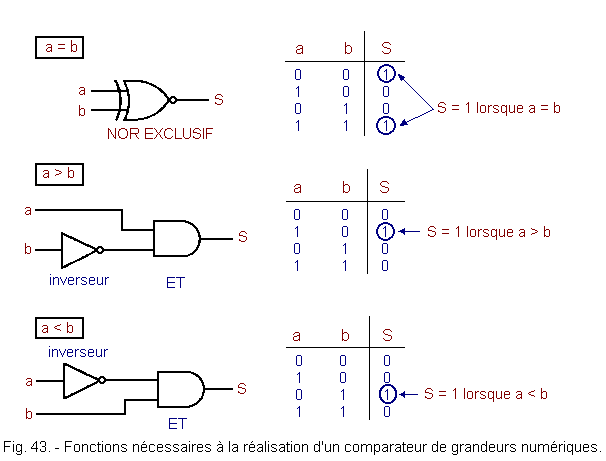
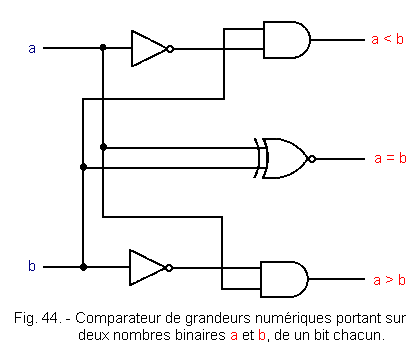
La figure 43 représente les fonctions logiques nécessaires à la réalisation d'un comparateur de grandeurs numériques. Ceci est résumé dans la figure 44 qui schématise un comparateur de grandeurs numériques portant sur deux nombres binaires a et b de un bit chacun.
Au début de ce chapitre, nous avions souhaité une seule procédure pour toutes les opérations. Maintenant que nous connaissons mieux le problème, voyons si l'on peut obtenir cette procédure, dans le cas d'une calculatrice très simplifiée, qui ne pourrait effectuer que des additions et des soustractions sur des entiers relatifs.
Dressons la liste des différentes opérations que cette machine devra réaliser.
-
 Position d'attente d'informations ou scrutation du clavier d'entrée.
Position d'attente d'informations ou scrutation du clavier d'entrée. -
 Entrée de la valeur absolue d'un nombre décimal à l'aide du clavier :
Entrée de la valeur absolue d'un nombre décimal à l'aide du clavier : -
 Transformation de cette valeur en binaire et mise en mémoire.
Transformation de cette valeur en binaire et mise en mémoire. -
 Entrée du signe affecté à cette valeur absolue :
Entrée du signe affecté à cette valeur absolue : -
 Signe +,
mettre le bit de signe à 0
Signe +,
mettre le bit de signe à 0 -
 Signe
-, effectuer le complément à 2.
Signe
-, effectuer le complément à 2. -
 Mémoriser le nombre signé obtenu en
Mémoriser le nombre signé obtenu en  et
et  .
. -
 Entrée d'un signe opérateur par le clavier. Mémoriser
ce signe.
Entrée d'un signe opérateur par le clavier. Mémoriser
ce signe. -
 Entrée du signe «=».
Départ de l'opération.
Entrée du signe «=».
Départ de l'opération. -
 Le signe reconnu en
Le signe reconnu en  est celui de l'addition :
est celui de l'addition : -
 Additionner les termes mémorisés en
Additionner les termes mémorisés en  .
. -
 Le signe reconnu en
Le signe reconnu en  est celui de la soustraction :
est celui de la soustraction : -
 Effectuer
le complément à 2
du dernier nombre
entré et additionner ce complément au premier terme entré.
Effectuer
le complément à 2
du dernier nombre
entré et additionner ce complément au premier terme entré. -
 Mémoriser ce résultat.
Mémoriser ce résultat. -
 Effectuer le test du bit de signe :
Effectuer le test du bit de signe : -
 S'il est égal à 0, le résultat est
positif, aucune modification sur le résultat mémorisé en
S'il est égal à 0, le résultat est
positif, aucune modification sur le résultat mémorisé en  .
. -
 S'il est
égal à 1, le résultat est négatif,
remplacer le terme mémorisé en
S'il est
égal à 1, le résultat est négatif,
remplacer le terme mémorisé en  par son complément à 2.
par son complément à 2. -
 Afficher le résultat mémorisé en
Afficher le résultat mémorisé en  .
.
La chronologie des opérations est donc celle représentée figure 45.
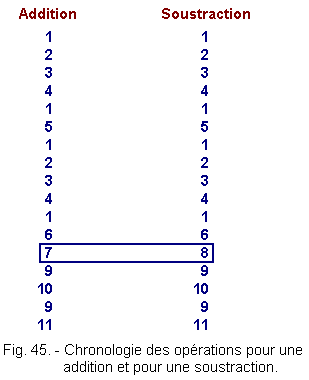
Il apparaît plus clairement que
seules, les opérations ![]() et
et ![]() sont quelque peu différentes entre l'addition et la soustraction. Il s'agit
d'une addition mais pour
sont quelque peu différentes entre l'addition et la soustraction. Il s'agit
d'une addition mais pour ![]() un des deux termes est complémenté à
2.
un des deux termes est complémenté à
2.
Si on voulait étendre les possibilités de cette machine à la multiplication et à la division, il faudrait introduire le décalage, le test de grandeur numérique et rechercher le rang du bit à 1 de poids le plus élevé.
La liste des opérations serait un peu plus longue, mais la rapidité avec laquelle elles sont effectuées ne différerait que de très peu de temps l'obtention du résultat.
Cette théorie est maintenant terminée. Nous vous rappelons que si vous n'avez pas parfaitement assimilé la partie concernant les calculs, ceci n'est pas d'une importance fondamentale pour la compréhension des leçons suivantes. Nous aurons d'ailleurs l'occasion d'y revenir dans les théories concernant les microprocesseurs.
La prochaine leçon traitera des
registres à décalage dont nous avons déjà évoqué le rôle dans cette théorie.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente |
 Page suivante Page suivante |
Nombre de pages vues, à partir de cette date : le 15 JUILLET 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.
 La soustraction
La soustraction