Caractéristiques du Courant Alternatif :
2. - CARACTÉRISTIQUES DU COURANT ALTERNATIF :
2. 1. - REPRÉSENTATION GRAPHIQUE DU COURANT ALTERNATIF
Essayons de déterminer l'allure du courant alternatif pour une rotation complète du flux d'induction. Nous savons déjà qu'au temps t = 0s et qu'au temps t = 4s sont intensité est nulle, il nous reste à trouver les différentes intensités prises par le courant entre ces deux temps.
Observons à ce propos la figure 3, le courant est nul lorsque les lignes du flux d'induction sont horizontales (figures 3-a et 3-e), alors qu'il circule dans tous les autres cas. D'autre part, de ce que nous savons sur la loi de LENZ, nous pouvons dire que l'intensité I du courant induit est maximale lorsque le flux embrassé par la spire est nul (cas des figures 3-c et 3-g).
De ces quatre positions connues, nous déduisons que l'intensité I du courant induit est fonction de l'angle formé entre les lignes du flux inducteur et l'horizontale.
Si nous symbolisons l'ensemble des lignes d'induction du flux par un vecteur (portion de droite orientée possédant une origine et une extrémité et dont la longueur est fonction de l'intensité de la force qu'il représente), ceci nous permet d'élaborer les différents cas de la figure 4.
L'origine du vecteur est le point 0 situé au centre de la spire. Faisons maintenant tourner le vecteur autour du point 0.
Les neuf cas de la figure 4-a déterminent neuf positions du vecteur par rapport à l'horizontal. En abaissant l'extrémité du vecteur sur un axe perpendiculaire à l'horizontal et passant par le point 0, nous obtenons neuf segments de droite d0 à d8 (dessinés en rouge sur la figure 4-a) dont la longueur est fonction de l'angle formé entre le flux d'induction et l'horizontale.
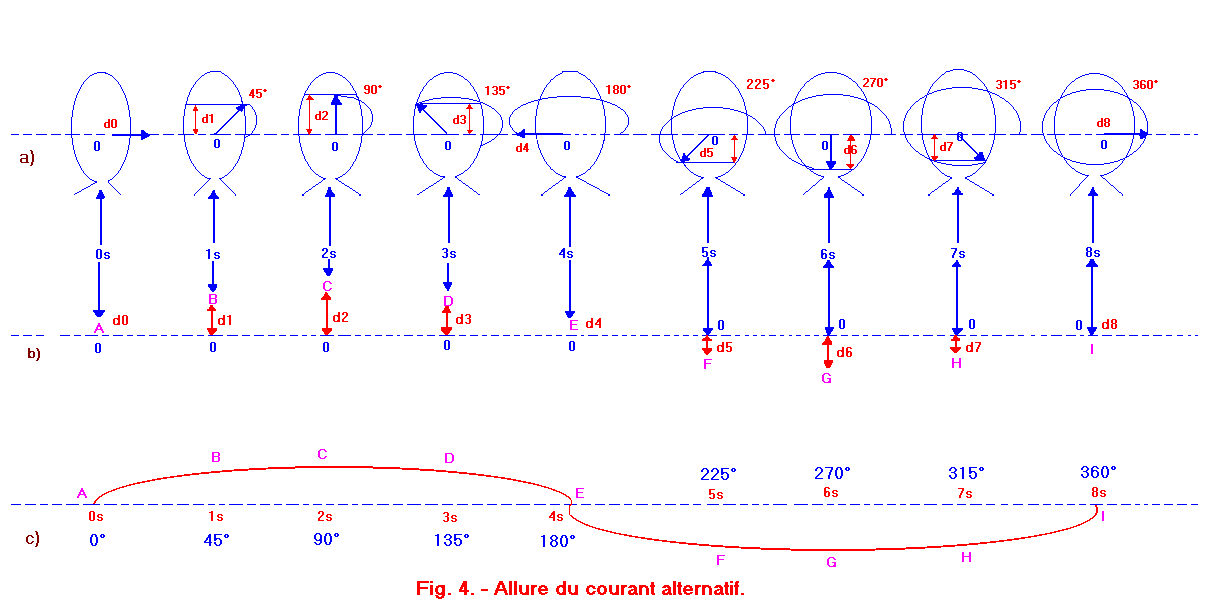
Ces neuf segments sont reportés seuls sur la figure 4-b et leurs extrémités respectives sont indiquées par les points A, B, C, D, E, F, G, H et I.
Lorsque le vecteur est horizontal, le segment de droite qu'il détermine est nul, ceci est le cas des segments OA (d0), OE (d4) et OI (d8). Figure 4-b, les points A, E et I sont confondus avec l'horizontale.
Lorsque le vecteur est perpendiculaire à l'horizontale, le segment de droite qu'il détermine est maximal et correspond à la longueur du vecteur, ceci est le cas des segments OC (d2) et OG (d6).
En fonction de ces données, déterminons l'allure du courant alternatif.
au temps t = 0s, le point A est confondu avec le point 0 (d0) : l'intensité du courant induit est nulle.
de t = 0s à t = 2s, le courant induit augmente et son intensité est maximale à t = 2s : le segment de droite OC (d2) est également maximal. Entre ces deux positions, le vecteur détermine au temps t = 1s le segment de droite OB (d1).
de t = 2s à t = 4s, le courant induit décroît et son intensité est nulle à t = 4s : le point E est confondu avec le point O (d4). Entre ces deux positions, plaçons
au temps t = 3s le point D correspondant au segment OD (d3). à t = 4s, le courant inverse son sens de circulation. de t = 4s à t = 6s, le courant induit augmente de nouveau et son intensité atteint un
deuxième maximum à t = 6s. Le segment de droite OG (d6) est maximal. Entre ces deux positions, plaçons au temps t = 5s le point F, déterminé par le segment OF (d5).
de t = 6s à t = 8s, le courant décroît et son intensité s'annule à t = 8s : le point I est confondu avec le point O (d8). à t = 8s, le sens du courant s'inverse à nouveau et un second cycle commence.
Les neuf points A, B, C,... que nous venons de déterminer et qui sont matérialisés sur la figure 4-b indiquent seulement la valeur de
l'intensité du courant prise à chaque seconde, mais rien n'indique la valeur prise par celle-ci à chaque instant. Pour obtenir le résultat désiré, il suffit de relier entre eux les neuf points connus en tenant compte du fait qu'entre chacun
de ces points le courant ne varie pas de façon linéaire. Les points ainsi réunis donnent la courbe représentée figure 4-c. Une courbe de cette allure porte le
nom de sinusoïde et nous dirons que le courant alternatif a une allure sinusoïdale. La sinusoïde, pouvant servir à indiquer à tout instant l'intensité prise par un courant alternatif, est donc utilisée pour la représentation graphique des
courants alternatifs sinusoïdaux dont un exemple est illustré figure 5. La droite horizontale pointillée de la figure 4-c est remplacée par une droite en trait continu où sont reportées les
secondes. Cette droite constitue l'échelle des temps sur laquelle un centimètre correspond à un temps d'une seconde. Cette droite est symbolisée par le sigle t (s) située à son extrémité droite. Le fait de
lire le temps sur une droite ne doit pas vous paraître étrange surtout lorsque l'on sait que nous lisons sur un cercle l'heure indiquée par une horloge ou par une montre. Puisque l'intensité du courant est matérialisée
par la distance entre chaque point de la sinusoïde et la droite horizontale, il est très utile de noter les valeurs de cette intensité sur une droite verticale perpendiculaire à l'échelle des temps. Cette droite constitue l'échelle
des courants sur laquelle un centimètre correspond à un ampère. Cette droite est symbolisée par le sigle I (A) situé à son extrémité supérieure. Notons que les deux droites
s'interceptent au point O de la figure 5. Ce point constitue l'origine de l'échelle des temps, mais par celle de l'échelle des courants car sur celle-ci apparaissent des chiffres précédés d'un signe "-", ce qui ne doit pas vous étonner vu que le courant alternatif circule dans deux sens différents. Les deux droites perpendiculaires sont également appelées axes et constituent avec la sinusoïde
un diagramme cartésien. Figure 5 sont reportés deux exemples d'utilisation de ce diagramme. Le premier exemple nous permet de déterminer l'intensité du courant après 1,5 secondes. Pour ceci reportons sur l'axe des temps le point A1, 1,5 cm après le point O (1 cm = 1s). De ce point A1, élevons
la perpendiculaire, celle-ci intercepte la sinusoïde au point A. La distance qui sépare les points A1 et A représente l'intensité que nous voulons connaître. Cette intensité peut se
lire sur l'axe des courants en traçant du point A une horizontale qui intercepte l'axe des courants au point A2. Sachant que sur cet axe 1 cm = 1A, il suffit
de mesurer la distance OA2 et de convertir le résultat en ampère. Nous trouvons dans ce cas 1,9 cm donc nous pouvons dire qu'au bout de 1,5 seconde l'intensité de I est de 1,9 A. La même procédure peut être adoptée pour notre second exemple, dans lequel nous désirons connaître l'intensité du
courant après 7,8 s. La différence avec le cas précédent est que le point B, obtenu sur la sinusoïde, détermine un point B2
situé sur l'axe des courants au-dessous du point O. Puisque la distance OB2 est de 0,7 cm, l'intensité du courant est de - 0,7 A
; le signe "-" précise que ce courant circule en sens contraire par rapport au courant considéré dans l'exemple précédent. Maintenant que nous savons représenter un courant alternatif, analysons ses caractéristiques ci-dessous, (paragraphe 2. 2.).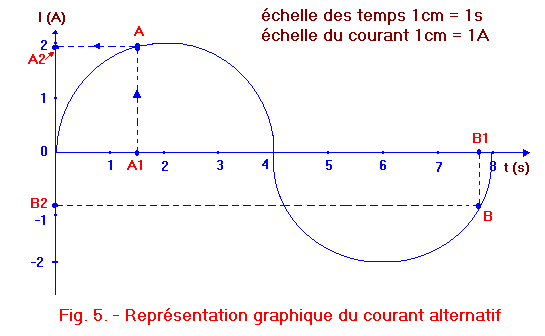
![]() 2. 2. -
PÉRIODE ET FRÉQUENCE DU COURANT ALTERNATIF
2. 2. -
PÉRIODE ET FRÉQUENCE DU COURANT ALTERNATIF
Jusqu'à présent, nous avons considéré que le flux d'induction n'effectuait qu'une seule rotation engendrant un courant dont l'allure est représentée figure 5.
Si le flux d'induction continue sa rotation et accomplit d'autres tours, chacun dans un temps identique, il engendrera à chaque tour un courant d'allure identique à celui de la figure 5. Un tour complet du flux détermine un cycle du courant alternatif.
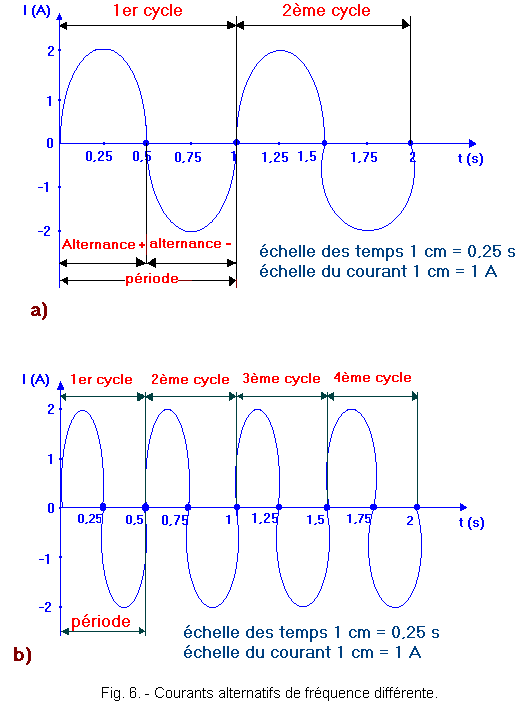
Le courant alternatif est une suite de cycles tous égaux entre eux ; ayant terminé un cycle, il en débute un suivant identique et cette succession donne la courbe représentée figure 6-a.
Du moment que tous les cycles sont identiques lorsque nous représentons graphiquement un courant alternatif, nous n'en dessinerons qu'un seul comme cela a été fait figure 5.
Pour faciliter nos explications précédentes, nous avions émis l'hypothèse que le flux d'induction effectuait une rotation complète en 8 secondes mais généralement, en pratique, celui-ci tourne beaucoup plus vite ; pour se rapprocher de la réalité, nous avons dans la figure 6-a choisi un temps de rotation de 1 seconde.
Pour permettre une analyse correcte d'un cycle complet, il nous a fallu changer d'échelle et figure 6-a, 1 cm de l'échelle des temps correspond, non plus à 1 seconde, mais à 0,25 s. Par contre, nous avons conservé la même échelle pour le courant, soit 1 cm pour 1 A.
De la comparaison des figures 5 et 6-a, il ressort que pour accomplir dans les deux cas un cycle identique, le courant de la figure 6-a met 1 seconde tandis qu'il en met 8 secondes dans la figure 5.
Nous venons d'établir ici une seconde caractéristique du courant alternatif, car pour que deux courants alternatifs soient égaux, il ne suffit pas qu'ils prennent les mêmes valeurs d'intensité, mais il faut que ces valeurs soient égales à chaque instant, autrement dit qu'ils effectuent un cycle complet dans le même temps.
On appelle période (symbole T) le temps mis par le courant alternatif pour accomplir un cycle complet. L'unité de la période est donc la seconde (symbole s).
Figure 6-a, la période du courant alternatif représentée est de 1s ; dans cette même figure, nous constatons que la période se divise en deux parties égales appelées alternance positive et alternance négative. Les deux alternances doivent leur nom aux valeurs des courants qu'elles déterminent sur l'échelle du courant (nombres positifs pour l'alternance positive et nombres négatifs pour l'alternance négative).
Le fait de diviser une période en deux alternances ne paraît pas évident. Toutefois, ceci devient une nécessité lorsque l'on sait que le courant circule dans un sens pendant l'alternance positive et dans le sens contraire durant l'alternance négative et que, comme nous le verrons dans les prochaines leçons, certains composants électroniques réagissent différemment selon le sens du courant qui les traverse.
Examinons maintenant le courant alternatif de la figure 6-b dont la période est de 0,5 s.
Si nous le comparons au courant de la figure 6-a, nous notons qu'il accomplit deux cycles pendant que celui de la figure 6-b n'en accomplit qu'un seul. De ceci, nous déduisons que pour un temps donné, plus la période est petite plus le nombre de cycles est grand.
Un courant alternatif peut aussi caractérisé par le nombre de cycles qu'il effectue en une seconde. On appelle fréquence (symbole F) le nombre de cycles accomplis par un courant alternatif en une seconde.
La fréquence F se mesure en cycles par seconde, unité à laquelle il est donné le nom de hertz (symbole Hz) en hommage au physicien allemand Heinrich HERTZ (1857-1894) dont les expériences mirent en évidence la propagation des ondes électromagnétiques.
Le courant de la figure 6-a possède une fréquence de 1 Hz puisqu'il accomplit 1 cycle en une seconde, tandis que celui de la figure 6-b possède une fréquence de 2 Hz vu que dans la même seconde il accomplit 2 cycles.
Le courant alternatif que nous utilisons dans les habitations à des fins domestiques possède une fréquence de 50 Hz, ce qui signifie qu'il accomplit 50 cycles en 1 seconde.
Dans certains appareils particuliers (comme les récepteurs radio ou les téléviseurs), il existe des courants qui accomplissent des milliers voire des millions de cycles par seconde, d'où la nécessité d'utiliser pour quantifier la fréquence non plus le hertz mais le kilohertz (symbole kHz) qui vaut 1 000 Hz ou le mégahertz (symbole MHz) égal à 1 000 000 Hz. Bien évidemment, des courants de fréquence aussi élevée ne s'obtiennent plus de la manière décrite jusqu'alors, c'est-à-dire en faisant tourner un flux d'induction : il n'est en effet pas possible de faire accomplir à un circuit inducteur des milliers ou des millions de tours par seconde. Pour la production de ces courants dits haute-fréquence (HF), nous aurons recours à des circuits particuliers : les oscillateurs électroniques.
Comme nous venons de le voir, la période et la fréquence sont intimement liées entre elles. Cette union est scellée par la relation suivante :
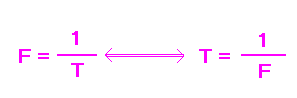
De cette relation, nous voyons que la période et la fréquence sont deux grandeurs inversement proportionnelles.
Appliquons cette formule pour calculer la période du courant alternatif du secteur :
T = 1 / F = 1 / 50 Hz = 0,02 s = 20 ms (millisecondes).
Nous savons maintenant que le courant alternatif du secteur met 20 ms pour accomplir un cycle complet. De même, si nous connaissons la période T d'un courant alternatif, par exemple 10 µs, en appliquant la relation sous sa forme F = 1 / T nous déduisons que ce courant possède une fréquence de 100 kHz.
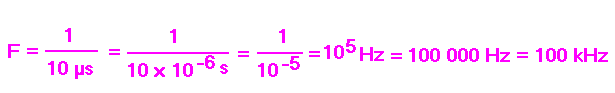
Il existe un troisième paramètre caractérisant le courant alternatif : il s'agit de sa pulsation (symbole ![]() se
lit oméga) et qui s'exprime en radians par seconde (rd / s). La pulsation s'obtient à l'aide de la relation :
se
lit oméga) et qui s'exprime en radians par seconde (rd / s). La pulsation s'obtient à l'aide de la relation :
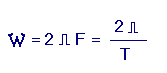
La pulsation caractérise la vitesse de rotation du vecteur symbolisant le flux inducteur dans la figure 4-a. Cette grandeur, comme vous le verrez dans de prochaines leçons, est principalement nécessaire pour les calculs relatifs à des circuits électriques alimentés par une tension alternative.
![]() 2. 3.
- VALEUR DU COURANT ALTERNATIF
2. 3.
- VALEUR DU COURANT ALTERNATIF
Pour représenter un courant alternatif, il faut indiquer sa fréquence et l'allure de la sinusoïde qui donne à chaque instant l'intensité du courant.
Nous observons cependant que l'intensité du courant varie constamment et nous ne savons quelle valeur choisir pour caractériser avec précision cette intensité : si nous considérons le courant alternatif représenté figure 7, la logique dicterait d'opter, pour la valeur maximale atteinte par le courant durant une période.
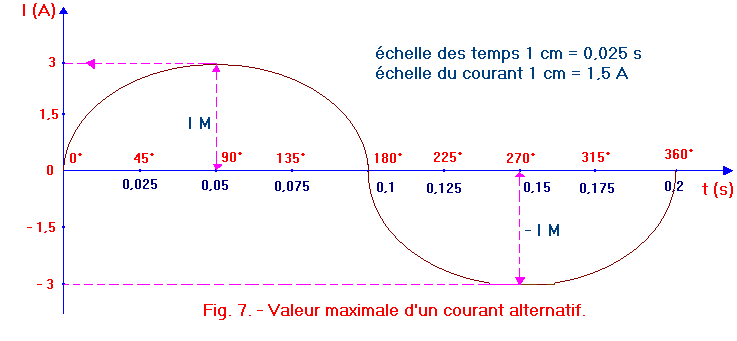
Cette valeur est atteinte deux fois par le courant : une première fois au milieu de l'alternance positive et une deuxième fois au milieu de l'alternance négative. Ces deux valeurs sont respectivement appelées IM et - IM. Cette valeur prise par le courant est appelée valeur maximale du courant alternatif.
Le diagramme cartésien de la figure 7 donne immédiatement la valeur IM du courant représenté qui est de 3 A. D'autre part, ce même diagramme nous permet de déterminer la fréquence de ce courant :
en effet, sa p&riode T = 0,2 s --------------) F = 1 / 0,2 = 5 Hz
Le courant alternatif de la figure 7 se caractérise par les deux paramètres suivants :
IM = 3A
F = 5 Hz
Toutefois, nous pouvons déterminer à chaque instant la valeur du courant en fonction de l'angle de rotation du flux
inducteur. En effet, une fonction sinusoïdale a pour équation y = ax dans laquelle x = sin ![]() (se
lit sinus phi).
(se
lit sinus phi).
Pour le cas qui nous intéresse,
![]() est
l'angle décrit par le flux inducteur et l'horizontale (figure 4-a) tandis que (a) est la valeur IM
du courant et que (y) donne la valeur instantanée (i) du courant à l'angle
est
l'angle décrit par le flux inducteur et l'horizontale (figure 4-a) tandis que (a) est la valeur IM
du courant et que (y) donne la valeur instantanée (i) du courant à l'angle ![]() considéré.
considéré.
Nous pouvons écrire :
i = IM sin![]()
A l'aide des figures 4-a et 7, appliquons cette équation pour déterminer certaines valeurs du courant.
![]() = 0°, sinus 0° = 0. Le courant i est donc nul, nous sommes au début du cycle.
= 0°, sinus 0° = 0. Le courant i est donc nul, nous sommes au début du cycle.
![]() = 90°, le flux a accompli un quart de tour, sin 90° = + 1 ------) i = IM
= 3 A.
= 90°, le flux a accompli un quart de tour, sin 90° = + 1 ------) i = IM
= 3 A.
![]() = 180°, le flux a accompli un demi-tour, sin 180° = sin 0° = 0. Le courant est nul.
= 180°, le flux a accompli un demi-tour, sin 180° = sin 0° = 0. Le courant est nul.
![]() = 270°, le flux a accompli trois quarts de tour. sin 270° = - 1 ---------) i = - IM = - 3 A.
= 270°, le flux a accompli trois quarts de tour. sin 270° = - 1 ---------) i = - IM = - 3 A.
![]() = 360°, le flux a accompli un tour complet. sin 360° = sin 0° = 0. Le courant est nul.
= 360°, le flux a accompli un tour complet. sin 360° = sin 0° = 0. Le courant est nul.
La valeur du sinus d'un angle est donnée par une table appelée table trigonométrique. Celle-ci donne le sinus d'un angle quelque soit sa valeur, et nous pouvons donc connaître la valeur du courant quelle que soit la position du flux par rapport à l'horizontale.
Étant donné que la valeur maximale du courant est atteinte deux fois par celui-ci, nous comprenons donc que cette valeur n'est peut-être pas très adaptée pour caractériser un courant alternatif, ne serait-ce que pour déterminer l'effet thermique produit par un tel type de courant. Cet effet du courant est indépendant de son sens de circulation : effectivement, pour qu'il y ait production de chaleur, il suffit qu'un courant traverse une résistance et peu importe qu'il circule dans un sens ou dans l'autre. La production de chaleur est la même pour chacune des deux alternances.
Pour évaluer l'effet thermique du courant, nous pouvons nous référer à une période entière. Nous pouvons appliquer alors la formule w = R x I2 x t dans laquelle t = T. Alors qu'il nous est facile de connaître R et T, nous ne savons quelle valeur de I choisir vu que celui-ci change constamment et en conséquence la valeur dégagée à chaque instant. Il faut donc faire intervenir une nouvelle caractéristique du courant alternatif qui est son intensité efficace symbolisée par le sigle Ieff.
L'intensité efficace d'un courant alternatif se traduit de la façon suivante :
C'est l'intensité d'un courant continu qui produirait dans la même résistance, la même quantité de chaleur que ce courant alternatif.
NOTE :
Compte tenu de cette définition, l'intensité efficace peut, selon le système international de mesure S.I., être symbolisée par la simple lettre I.
Il existe une relation entre l'intensité efficace et l'intensité maximale d'un courant sinusoïdal.
Cette relation correspond au rapport :
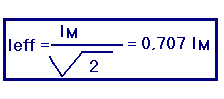
NOTE :
La démonstration de cette relation faisant appel à des connaissances mathématiques sortant de notre programme, nous n'en parlerons donc pas. Outre la valeur maximale et la valeur efficace d'un courant alternatif, il existe aussi sa valeur moyenne (symbole Imoy) qui se définit ainsi :
L'intensité moyenne d'un courant alternatif est l'intensité du courant continu qui transporterait pendant l'intervalle de temps considéré (une période) la même quantité d'énergie.
Dans le cas d'un courant alternatif sinusoïdal, la valeur moyenne d'une alternance est donnée par la relation :
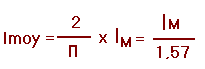
Si nous calculons la valeur moyenne pour un période complète, nous trouvons une valeur nulle.
Pour expliquer ceci succinctement, il suffit de penser que les électrons, lors de l'alternance positive, se déplacent dans un sens, et que lors de l'alternance négative ces mêmes électrons refont le même chemin dans l'autre sens et reviennent à leur point de départ ; donc la quantité d'énergie fournie par le générateur est nulle (mais pas celle nécessaire à son fonctionnement, qui elle, est bien réelle).
Le type de courant que nous avons choisi pour nos explications est un courant alternatif de valeur moyenne nulle comme celui délivré par le secteur, mais comme vous le verrez par la suite il existe des courants alternatifs de valeur moyenne non nulle d'où la nécessité d'avoir introduit cette notion.
Tout au long de cette leçon, nous avons vu comment représenter graphiquement un courant alternatif et comment à partir de ce graphique il nous est possible de déterminer toutes les caractéristiques d'un tel courant.
Les grandeurs relatives au courant alternatif sinusoïdal sont regroupées dans le tableau de la figure 8.
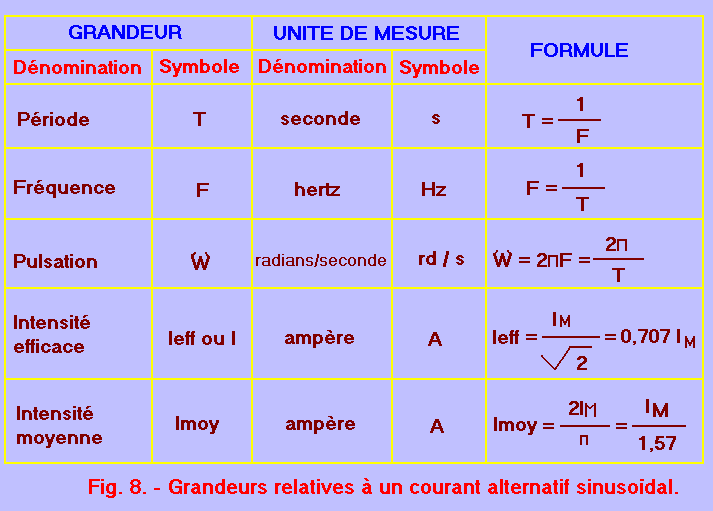
Dans la prochaine leçon, nous analyserons non plus le courant alternatif mais la tension alternative et nous verrons les relations qui lient ces deux grandeurs selon le type de circuits qu'elles alimentent.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente |
 Page suivante Page suivante |
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.
 Période et fréquence du courant alternatif
Période et fréquence du courant alternatif
