 Bas de page Bas de page |
Impédance et Puissance Électrique :
Cette leçon traite, dans un premier temps, de l'impédance électrique d'une bobine inductrice.
Dans un second chapitre, nous allons examiner la puissance électrique en courant alternatif.
Enfin, la dernière partie est consacrée à l'analyse des circuits magnétiques.
1. - IMPÉDANCE
Nous allons commencer cette nouvelle théorie en examinant les inductances.
Une inductance, ou bobine, est un enroulement constitué de nombreuses spires d'un fil conducteur, généralement de faible section.
Ces inductances sont des obstacles au passage du courant. Si le courant considéré est continu, on dit qu'elles offrent une résistance ; s'il est alternatif, on parle alors de réactance et, plus précisément dans le cas des inductances, de réactance inductive.
La résistance est une grandeur que nous connaissons déjà. C'est la résistance ohmique du conducteur. Son symbole est évidemment R et elle s'exprime en ohms.
La réactance, qui n'apparaît que lorsque la bobine est parcourue par un courant alternatif, est fonction d'une caractéristique propre de la bobine, appelée coefficient de self-induction et symbolisé par la lettre L, et de la fréquence du courant alternatif. Comme la résistance, elle s'exprime en ohms.
Lorsque la valeur de la résistance est faible par rapport à celle de la réactance, on la néglige. Dans ce cas, l'inductance est représentée schématiquement comme le montre la figure 1-a.
Si l'on veut au contraire considérer la valeur de la résistance R, le schéma équivalent de l'inductance est celui représenté figure 1-b.
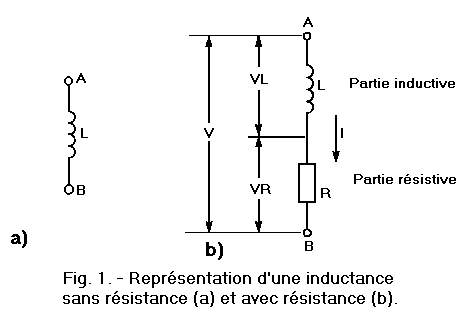
Le symbole d'une inductance résistive permet de considérer l'inductance réelle comme étant constituée d'une inductance sans résistance ohmique (L) associée en série avec une résistance pure (R).
Les bornes réelles de l'inductance résistive sont A et B (figure 1-b). La tension V, appliquée aux bornes A et B, se répartit aux bornes de L et de R qui forment un diviseur de tension. On obtient ainsi aux bornes de chacun de ces éléments les tensions VL et VR.
On pourrait donc penser qu'entre les extrémités A et B de l'inductance, il faut appliquer une tension V dont la valeur efficace est la somme des valeurs efficaces de VL et de VR.
En fait, il n'en est pas ainsi car les tensions VL et VR n'ont pas la même phase par rapport au courant comme le montre la figure 2.
Deux périodes (ou cycles) du courant sont représentées figure 2-a, la deuxième est représentée par un trait plus accentué. La tension VR, nécessaire pour la partie résistive, est représentée figure 2-b, durant deux périodes également.
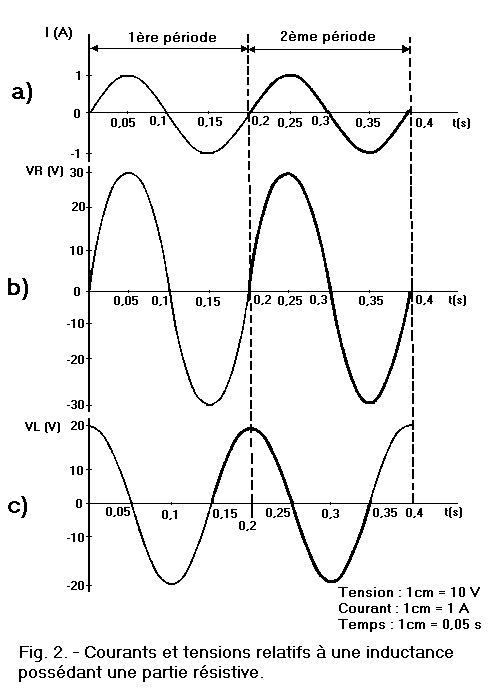
Il apparaît que VR est en phase avec le courant I. La tension VL est représentée figure 2-c.
Le trait gras indique une période (ou un cycle) complète. Cette tension VL est déphasée d'un quart de période par rapport à VR ou à I.
Elle débute un quart de période avant VR et se termine également un quart de période avant VR.
Ainsi, la tension VL apparaissant aux bornes de la bobine (inductance) est déphasée en avance d'un quart de période par rapport à la tension VR.
Par suite de ce déphasage, à l'instant où l'une des deux tensions atteint la valeur maximale, l'autre atteint la valeur zéro et inversement ; en effet, en comparant les figures 2-b et 2-c, on s'aperçoit, par exemple, qu'au temps 0 seconde correspondent les tensions VR nulle et VL maximale ; au contraire, au temps de 0,05 seconde correspondent une tension VL nulle et une tension VR maximale.
Au temps 0 seconde, la tension V appliquée entre les extrémités A et B de la bobine est égale à la valeur maximale de VL puisque VR est nulle à cet instant. Par contre, au temps 0,05 seconde, V est égale à la valeur maximale de VR puisque VL est nulle.
La valeur maximale de V n'est donc pas égale à la somme des valeurs maximales des tensions VL et VR car ces deux valeurs maximales sont atteintes à des instants différents.
Pour calculer la tension V, il faut avoir recours à la représentation vectorielle, qui permet de mettre en évidence le déphasage entre VL et VR.
La figure 3 représente vectoriellement les tensions VR, VL et le courant I. Ces représentations sont les mêmes que celles déjà vues pour le circuit ohmique et pour le circuit inductif.
Les éléments L et R étant en série, ils sont parcourus par le même courant I. Nous prendrons donc le vecteur représentant ce courant comme vecteur de référence.
Nous savons que dans une résistance pure, courant et tension sont en phase. Les deux vecteurs les représentant seront donc sur le même axe (figure 3-a).
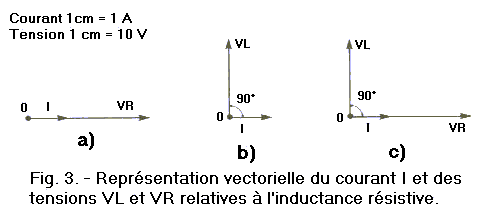
Nous venons de voir que dans une inductance pure, la tension VL est déphasée d'un front de période en avance sur VR. Comme VR est en phase avec I, on peut également dire que VL est en avance sur IR. Un quart de période correspondant à 90°, la représentation vectorielle de VL par rapport à I sera celle de la figure 3-b.
Nous pouvons enfin représenter sur un même graphique les différentes valeurs représentées figures 3-a et 3-b. Nous obtenons ainsi la figure 3-c.
Pour trouver le vecteur représentant la tension V, il faut effectuer la somme vectorielle des deux vecteurs représentant VR et VL. On tient ainsi compte des valeurs maximales de VR et VL et du déphasage entre ces deux tensions.
La figure 4-a, indique la somme des deux vecteurs VL et VR. Nous remarquons que le sens, la direction et la longueur des vecteurs sont identiques à ceux de la figure 3-c. Le déphasage est toujours égal à 90°. Il suffit de réunir les extrémités O et A des deux vecteurs pour obtenir celui représentant la tension V.
.gif)
Pour calculer la valeur de V, il suffit de tenir compte du fait qu'un centimètre représente 10 volts.
(Si vous avez oublié ce théorème de Pythagore, cliquez sur le lien ci-contre). Théorème de Pythagore.
Le vecteur VL (2 cm de long) représente une tension de 20 volts, tandis que le vecteur VR (3 cm de long) représente une tension de 30 volts.
En mesurant sur la figure la longueur du vecteur V, nous voyons qu'elle est de 3, 6 cm et que, par conséquent, la tension V vaut 36 volts.
Nous pouvons conclure que la tension V à appliquer aux bornes de la bobine pour qu'elle soit parcourue par un courant de 1 A, a la valeur maximale de 36 volts.
Il est également possible de calculer cette valeur en appliquant le théorème de Pythagore au triangle rectangle formé par les trois vecteurs.
Faisons un bref rappel de ce théorème à l'aide de la figure 4-b.
Les côtés AB et AC sont les côtés de l'angle droit ; BC, qui est le plus long, est l'hypoténuse.
Selon le théorème de Pythagore, en faisant la somme des carrés des longueurs des côtés de l'angle droit, on obtient le carré de la longueur de l'hypoténuse.
Dans le cas de la figure 4-b, on a :
42 + 32 = 16 + 9 = 25 = 52
Ce théorème peut être appliqué au schéma de la figure 4-a :
302 + 202 = 900 + 400 = 1 300
Ce nombre 1 300, est donc le carré de la valeur maximale de V.
La racine carrée de 1 300 est 36,055. Nous retrouvons bien la même valeur que celle mesurée précédemment (36 volts).
Nous savons que la valeur maximale d'une tension alternative est égale à 1,41 fois sa valeur efficace.
Nous pouvons donc dire que la valeur efficace de la tension que l'on doit appliquer aux extrémités d'une bobine est égale à la racine carrée du nombre obtenu en faisant la somme des carrés des valeurs efficaces des tensions nécessaires pour la partie inductive et pour la partie ohmique de cette bobine.
Nous avons déjà dit que la partie résistive et la partie inductive constituent un obstacle au passage du courant dans la bobine. Cet obstacle est appelé impédance électrique et on l'indique symboliquement par la lettre Z.
L'impédance électrique se mesure en ohms, comme la résistance et la réactance.
Cette impédance s'exprime par la relation suivante :
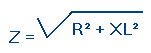
XL est la réactance de la partie inductive. Pour déterminer cette relation, il faut partir de la relation : V2 = VR2 + VL2 (application du théorème de Pythagore).
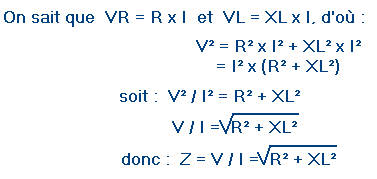
Ainsi, la loi d'OHM s'applique à une bobine résistive, tout comme elle s'appliquait à une résistance et à une inductance pure.
La valeur de la tension nécessaire pour qu'un courant alternatif déterminé traverse une bobine s'obtient en multipliant ce courant par l'impédance qu'elle présente.
Il nous reste à voir le déphasage existant entre cette tension et le courant.
(Pour en faciliter la lecture, nous reportons le même schéma à savoir figure 4) :
.gif)
Sur la figure 4-a, pour trouver le vecteur V, nous avons dessiné le vecteur VR horizontalement, puis le vecteur VL verticalement, à l'extrémité de VR.
Nous pouvons également adopter la procédure indiquée figure 5-a, c'est-à-dire dessiner horizontalement le vecteur VR puis verticalement le vecteur VL. En reliant ensuite les points O et A, on obtient le vecteur V en tout point identique à celui de la figure 4-a.
Le vecteur V peut aussi se déduire directement de la figure 3-c, ce qui est indiqué figure 5-b.
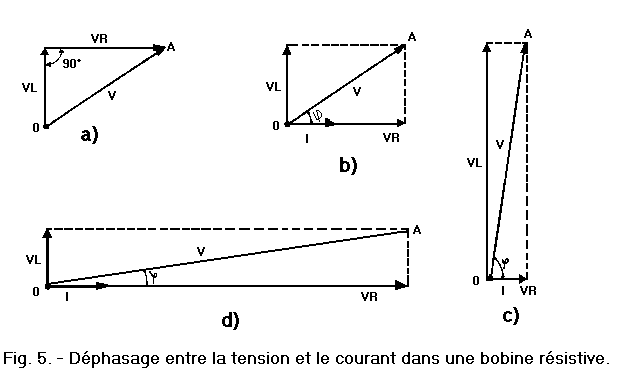
Pour situer le point A, il suffit de tracer deux parallèles aux vecteurs VL et VR ; elles sont indiquées en pointillé sur cette figure 5-b. Cette nouvelle méthode présente l'avantage de mettre en évidence le déphasage existant entre V et I.
Ce déphasage correspond à l'angle ![]() "phi" (
"phi" (
![]() est la lettre minuscule qui correspond à la lettre
est la lettre minuscule qui correspond à la lettre ![]() qui est une lettre majuscule de l'alphabet grec). Nous notons que cet angle
qui est une lettre majuscule de l'alphabet grec). Nous notons que cet angle
![]() est inférieur à 90°.
est inférieur à 90°.
Cela signifie qu'une bobine résistive possède des caractéristiques intermédiaires entre celles
d'une résistance pure (
![]() = 90°).
= 90°).
L'angle de déphasage est donc proportionnel au rapport de la réactance sur la résistance.
La figure 5-c représente ce déphasage dans le
cas où la réactance est très supérieure à la résistance. Dans ce cas,
l'angle ![]() est proche de 90°.
est proche de 90°.
Sur la figure 5-d, c'est le cas contraire qui est représenté ; l'angle ![]() est proche de 0° car la réactance est très faible par rapport à la valeur de la résistance.
est proche de 0° car la réactance est très faible par rapport à la valeur de la résistance.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet.
|
|
 Page précédente Page précédente
|
 Page suivante Page suivante
|
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.

